Repeat Problem 10.D9, part a only, except at \(1.50 \mathrm{~atm}\). The Antoine equation constants to determine the vapor pressure of methanol are in Table 2-3. Other physical properties are in Problem 10.D9. VLE data are in Table 2-8.

Problem 10.D9

\(1000.0 \mathrm{kmol} / \mathrm{h}\) of a saturated vapor feed that is \(60.0 \mathrm{~mol} \%\) methanol and \(40.0 \mathrm{~mol} \%\) water is distilled in a sieve plate column operating at \(75 \%\) of flooding velocity. Distillate is \(99.9 \mathrm{~mol} \%\) methanol, and bottoms is \(1.0 \mathrm{~mol} \%\) methanol. \(\mathrm{L} / \mathrm{V}=0.6\) and \(\mathrm{p}=1.0 \mathrm{~atm}\). Use a \(0.4572-\mathrm{m}\) tray spacing and \(\eta=0.90\). Density of pure liquid methanol is \(0.7914 \mathrm{~g} / \mathrm{ml}\). Data are available in Table 2-8 and Table 2-3. Assume an ideal gas. The surface tension of pure methanol can be estimated as \(\sigma=\) \(24.0-0.0773 \mathrm{~T}\) with \(\mathrm{T}\) in \({ }^{\circ} \mathrm{C}\) (Dean, 1985, p. 10-110).

a. Calculate the diameter based on the conditions at the top of the column.

b. Calculate \((\mathrm{L} / \mathrm{D})_{\min }\) and multiplier \(\mathrm{M}=(\mathrm{L} / \mathrm{D}) /(\mathrm{L} / \mathrm{D})_{\min }\).

Table 2-3

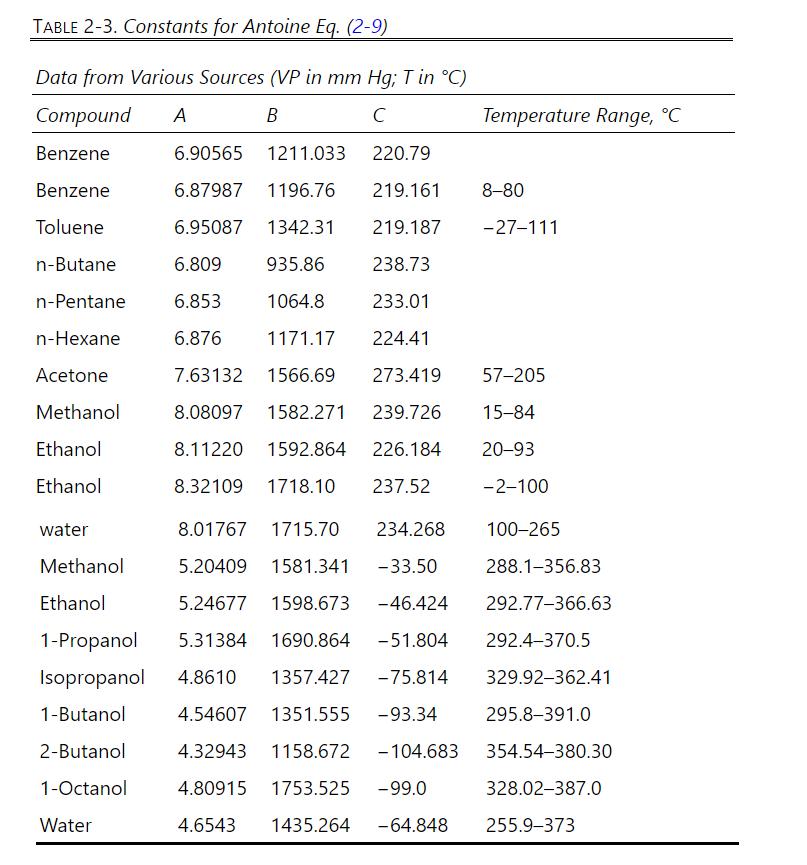
Table 2-8

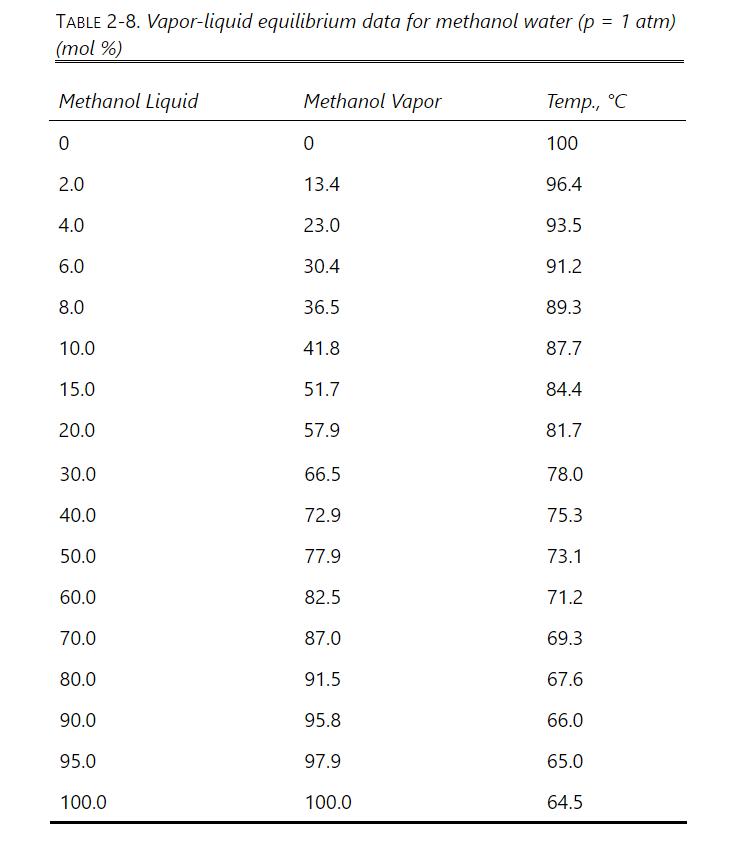
TABLE 2-3. Constants for Antoine Eq. (2-9) Data from Various Sources (VP in mm Hg; T in C) Compound A B C Temperature Range, C Benzene 6.90565 1211.033 220.79 Benzene 6.87987 1196.76 219.161 8-80 Toluene 6.95087 1342.31 219.187 -27-111 n-Butane 6.809 935.86 238.73 n-Pentane 6.853 1064.8 233.01 n-Hexane Acetone Methanol 6.876 7.63132 1566.69 273.419 239.726 1171.17 224.41 57-205 Ethanol Ethanol 8.08097 1582.271 8.11220 1592.864 226.184 20-93 8.32109 1718.10 237.52 15-84 -2-100 water Methanol 8.01767 1715.70 234.268 100-265 5.20409 1581.341 -33.50 288.1-356.83 Ethanol 5.24677 1598.673 -46.424 292.77-366.63 1-Propanol 5.31384 1690.864 -51.804 292.4-370.5 1-Butanol 2-Butanol Isopropanol 4.8610 1357.427 -75.814 329.92-362.41 295.8-391.0 4.54607 1351.555 -93.34 4.32943 1158.672 -104.683 354.54-380.30 1-Octanol Water 4.80915 1753.525 -99.0 328.02-387.0 4.6543 1435.264 -64.848 255.9-373