Repeat Problem 15.H1, but bulb 1 at \(\mathrm{z}=0\) contains the following mole fractions: \(\mathrm{y}_{\text {air }}\) \(=0.520, \mathrm{y}_{\mathrm{H} 2}=0.480\), and \(\mathrm{y}_{\mathrm{NH} 3}=0.000\). Bulb 2 at \(\mathrm{z}=\delta\) contains \(\mathrm{y}_{\text {air }}=0.520, \mathrm{y}_{\mathrm{H} 2}=\) 0.000 , and \(\mathrm{y}_{\mathrm{NH} 3}=0.480\).

Problem 15.H1

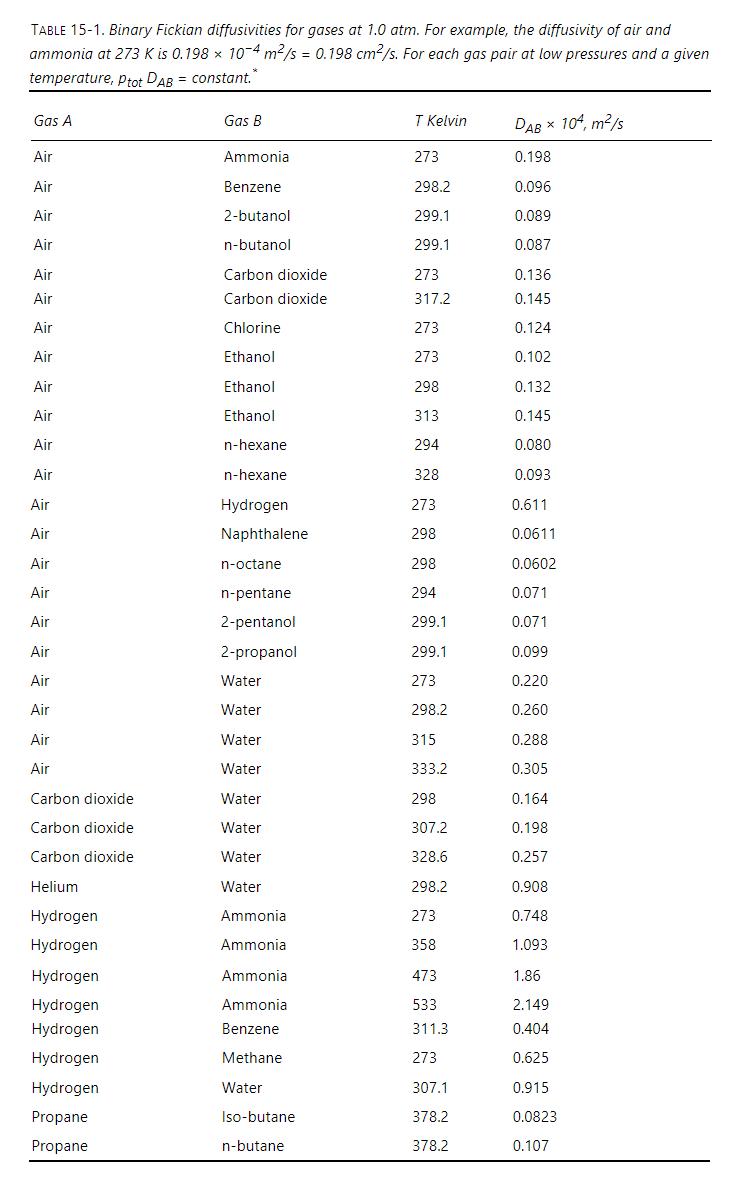
Two identical large glass bulbs are filled with gases and connected by a capillary tube that is \(\delta=0.0100 \mathrm{~m}\) long. Bulb 1 at \(\mathrm{z}=0\) contains the following mole fractions: \(\mathrm{y}_{\text {air }}=\) \(0.520, \mathrm{y}_{\mathrm{H} 2}=0.480\), and \(\mathrm{y}_{\mathrm{NH} 3}=0.000\). Bulb 2 at \(\mathrm{z}=\delta\) contains \(\mathrm{y}_{\text {air }}=0.540, \mathrm{y}_{\mathrm{H} 2}=\) 0.000 , and \(y_{\mathrm{NH} 3}=0.460\). Because the bulbs are quite large, operation is at pseudo- (or quasi-) steady state. (In other words, assume mole fractions at the boundaries are constant [e.g., \(\mathrm{y}_{\text {air }}=0.520\) at \(\mathrm{z}=0\), and \(\mathrm{y}_{\text {air }}=0.540\) at \(\mathrm{z}=\delta\) so that \(\Delta \mathrm{y}_{\text {air }}=0.02\) ] and total flux of air + hydrogen + ammonia is zero.) Pressure is uniform at \(2.00 \mathrm{~atm}\), and temperature is uniform at \(273 \mathrm{~K}\). Diffusivity values can be determined from Table 151. Assume ideal gases. Estimate fluxes of the three components using difference equation formulation of the Maxwell-Stefan method.

Table 15-1

Transcribed Image Text:

TABLE 15-1. Binary Fickian diffusivities for gases at 1.0 atm. For example, the diffusivity of air and ammonia at 273 K is 0.198 x 10-4 m2/s = 0.198 cm/s. For each gas pair at low pressures and a given temperature, Ptot DAB = constant." Gas A Gas B T Kelvin DAR 104 m/s Air Air * * * * * * * * * * * * * * Air Ammonia 273 0.198 Air Benzene 298.2 0.096 Air 2-butanol 299.1 0.089 Air n-butanol 299.1 0.087 Air Carbon dioxide 273 0.136 Air Carbon dioxide 317.2 0.145 Air Chlorine 273 0.124 Air Ethanol 273 0.102 Air Ethanol 298 0.132 Air Ethanol 313 0.145 Air n-hexane 294 0.080 Air n-hexane 328 0.093 Hydrogen 273 0.611 Naphthalene 298 0.0611 Air n-octane 298 0.0602 Air n-pentane 294 0.071 Air 2-pentanol 299.1 0.071 Air 2-propanol 299.1 0.099 Air Water 273 0.220 Air Water 298.2 0.260 Air Water 315 0.288 Air Water 333.2 0.305 Carbon dioxide Water 298 0.164 Carbon dioxide Water 307.2 0.198 Carbon dioxide Water 328.6 0.257 Helium Water 298.2 0.908 Hydrogen Ammonia 273 0.748 Hydrogen Ammonia 358 1.093 Hydrogen Ammonia 473 1.86 Hydrogen Ammonia 533 2.149 Hydrogen Benzene 311.3 0.404 Hydrogen Methane 273 0.625 Hydrogen Water 307.1 0.915 Propane Iso-butane 378.2 0.0823 Propane n-butane 378.2 0.107