We are continuing our efforts to concentrate syrup for a food company by using a cellulose acetate RO membrane to concentrate a dilute sucrose mixture. Operation is at \(25.0^{\circ} \mathrm{C}\).

a. We measure pure water flux (no sucrose present) and find at a pressure drop of 102.0 atm across the membrane, \({ }^{\prime}{ }_{\text {solv }}^{\prime}=1.5 \times 10^{-3}\left[\mathrm{~g} /\left(\mathrm{cm}^{2} \mathrm{~s}\right)\right]\). An experiment in a highly stirred system \((M=1.0)\) with a dilute sucrose solution gives a rejection \(\mathrm{R}^{0}=0.997\) for an inlet weight fraction of 0.050 , and cut \(\theta^{\prime}=0.45\) (in weight units). Find \(\mathrm{K}_{\text {solv }}^{\prime} / \mathrm{t}_{\mathrm{ms}}\) and selectivity \(\alpha^{\prime}\).

b. We will design a perfectly mixed RO system to operate at conditions where \(M=3.0\). Feed is \(2.0 \mathrm{wt} \%\) sucrose. We want a cut of \(\theta^{\prime}=2 / 3\). Feed rate will be \(5.0 \mathrm{~kg} / \mathrm{s}\). Pressure drop across the membrane is 78.0 atm. Plot the RT curve, Eq. (19-19a), and find the intersection with the operating line, Eq. (19-22), to find \(\mathrm{x}_{\mathrm{p}}\) and \(\mathrm{x}_{\mathrm{r}}=\mathrm{x}_{\text {out }}\). This is a completely nonlinear (except for linearizing osmotic pressure dependence on sucrose concentration) result. Then find \(\mathrm{J}_{\text {solv }}^{\prime}\) and the membrane area.

c. Resolve part \(b\) for \(x_{p}\) and \(x_{\text {out }}\) using linearized solution Eq. (19-29a) with Eqs. (19-25a) and (19-25b).

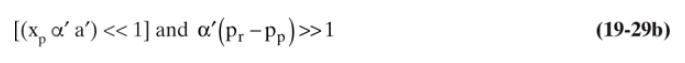
d. Compare your answers in parts \(\mathrm{b}\) and \(\mathrm{c}\). Which answer is more accurate?

Data are in Problem 19.D4.

Data From Problem 19.D4.

You are working on a low-temperature and energy-efficient method of concentrating syrup for a sugar company. Initial experiments are done with aqueous sucrose solutions and an RO system with a cellulose acetate membrane at \(25.0^{\circ} \mathrm{C}\).

Data: Density of solvent (water) is \(ho=0.997 \mathrm{~kg} / \mathrm{L}\).

Density ( \(\mathrm{kg} / \mathrm{L}\) ) of dilute aqueous sucrose solutions is \(ho=0.997+0.4 \mathrm{x}\) where \(\mathrm{x}\) is weight fraction sucrose.

At low sucrose weight fraction, osmotic pressure (in atm) at \(\mathrm{T}=25^{\circ} \mathrm{C}\) can be estimated as \(\pi=59.895 \mathrm{x}\) where \(\mathrm{x}\) is the weight fraction sucrose.

Molecular weight of water is 18.016 . Molecular weight of sucrose is 342.3 .

Experiment A. This experiment is done in a well-mixed stirred tank. At \(1000.0 \mathrm{rpm}\) with a \(3.0 \mathrm{wt} \%\) solution of sucrose in water using \(p_{r}=75.0 \mathrm{~atm}\) and \(p_{p}=2.0 \mathrm{~atm}\), we obtain \(J_{\text {solv }}^{\prime}=4.625 \mathrm{~g} /\left(\mathrm{m}^{2} \mathrm{~s}\right)\). Mass transfer coefficient \(\mathrm{k}=6.94 \times 10^{-5} \mathrm{~m} / \mathrm{s}\). We measure \(\mathrm{x}_{\mathrm{r}}=\mathrm{x}_{\text {out }}=0.054\) and \(\mathrm{x}_{\mathrm{p}}=3.6 \times 10^{-4}\).

Transcribed Image Text:

x Xr Xp[xp (a'a'-1)+(PP)+1] M[1+(a'a'-1)xp] (19-19a)