Write the divergence of the dyad (ho boldsymbol{v} boldsymbol{v}) in index notation. Expand the derivatives using the
Question:
Write the divergence of the dyad \(ho \boldsymbol{v} \boldsymbol{v}\) in index notation. Expand the derivatives using the chain rule.
Write the continuity equation in index notation and use this in the expanded expression for the divergence of the above dyad. Simplify and show that the result is \((\boldsymbol{v} \cdot abla) \boldsymbol{v}\). Hence verify that Eq. (5.5) is the same as Eq. (5.2).

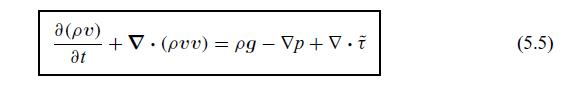
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Advanced Transport Phenomena Analysis Modeling And Computations
ISBN: 9780521762618
1st Edition
Authors: P. A. Ramachandran
Question Posted:





