For the reaction system: where (r_{1}=k_{1} C_{mathrm{A}}, r_{2}=k_{2} C_{mathrm{C}}, r_{3}=k_{3} C_{mathrm{A}}); and (r_{4}=k_{4} C_{mathrm{A}}). The rate constants

Question:

For the reaction system:

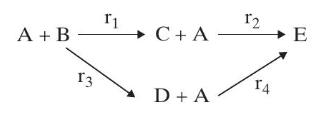
image text in transcribed

where \(r_{1}=k_{1} C_{\mathrm{A}}, r_{2}=k_{2} C_{\mathrm{C}}, r_{3}=k_{3} C_{\mathrm{A}}\); and \(r_{4}=k_{4} C_{\mathrm{A}}\). The rate constants are \(k_{1}=\mathrm{a} \min ^{-1}, k_{2}=\mathrm{b} \min ^{-1}, k_{3}=\mathrm{c} \min ^{-1}, k_{4}=\mathrm{d} \mathrm{min}^{-1}\), and the feed concentration of \(\mathrm{A}\) is \(1 \mathrm{kgmol} / \mathrm{m}^{3}\). Use the attainable region algorithm to find the reactor network that maximizes the selectivity of \(\mathrm{C}\) from A.

Fantastic news! We've Found the answer you've been seeking!