a. Example 8-1: Trambouze Reactions Wolfram 1. Fix k 2 at 0.015 and then describe how the
Question:
a. Example 8-1: Trambouze Reactions
Wolfram
1. Fix k2 at 0.015 and then describe how the selectivity varies with k1 and k3.
2. Write a conclusion about your experiments.
Polymath
3. What would have been the selectivity, SB/XY, and conversion, X, if the reaction had been carried out in a single PFR with the same volume as the CSTR?
4. Recalling CA0 = P0 RT, how would your answers change if the pressure were increased by a factor of 100?
Example 8-1
Reactant A decomposes by three simultaneous reactions to form three products, one that is desired, B, and two that are undesired, X and Y. These liquid-phase reactions, along with the appropriate rate laws, are called the Trambouze reactions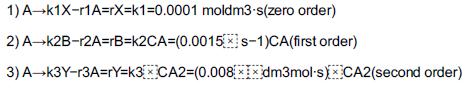
The Famous Trambouze Reactions
The specific reaction rates are given at 300 K and the activation energies for reactions (1), (2), and (3) are E1 = 10000 cal/mole, E2 = 15000 cal/mole, and E3 = 20000 cal/mole.
1. How, and under what conditions (e.g., reactor type(s), temperature, concentrations), should the reaction be carried out to maximize the selectivity of species B for
an entering concentration of species A of 0.4 M and a volumetric flow rate of 2.0 dm3/s?
2. How could the conversion of B be increased and still keep selectivity relatively high?
b. Example 8-2: Reactor Choice. Make a table/list for each reactor shown in Figure 8-2, identifying all the types of reactions that would be best carried out in this reactor. For example, Figure 8-2(d) Semibatch: used for
(1) highly exothermic reactions
(2) increased selectivity.
Figure 8-2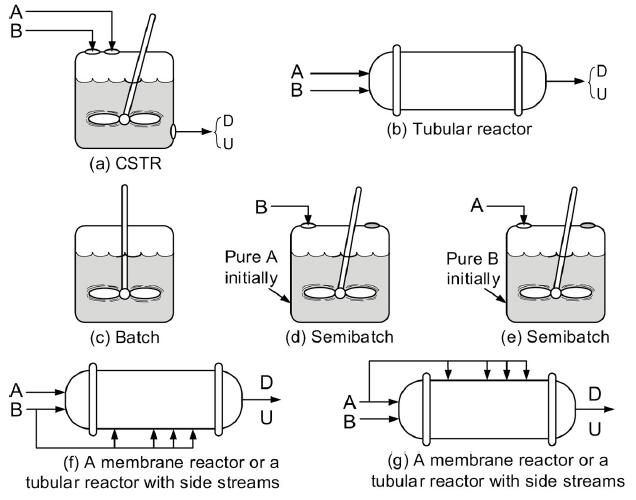
Example 8-2
For the parallel reactions
A + B→D:rD=k1CAα1CBβ1A + B→U:rU=k2CAα2CBβ2
consider all possible combinations of reaction orders and select the reaction scheme that will maximize SD/U.
c. Example 8-3: LEP Series Reactions in Batch Reactor
Wolfram and Polymath
1. Describe how the trajectories CA, CB, CC, SB/C, and YB/C change by setting E1 and E2 equal to zero and then varying k1 and k2 from their maximum to minimum values.
2. Fix T at 450 K and then vary E1 and E2, and describe how selectivity and conversion vary.
3. Write a set of conclusions about your experiment in (i)–(ii) above.
Example 8-3
The elementary liquid-phase series reaction
A→k1B→k2C
is carried out in a batch reactor. The reaction is heated very rapidly to the reaction temperature, where it is held at this temperature until the time it is quenched by rapidly lowering the temperature.
1. Plot and analyze the concentrations of species A, B, and C as a function of time.
2. Calculate the time to quench the reaction when the concentration of B will be a maximum.
3. What are the overall selectivity and yields at this quench time?
Additional Information
d. Example 8-4: LEP Series Reactions in a CSTR
Wolfram and Python
1. Use Wolfram to describe how the trajectories CA, CB, CC, SB/C, and YB/C change by setting E1 and E2 equal to zero and then varying k1 and k2 from their maximum to minimum values.
2. Write a set of conclusions about your experiment in (i) above.
Polymath
3. What CSTR operating temperature (with t = 0.5 s) would you recommend to maximize B for CA0 = 5 mol/dm3, k1 = 0.4 s–1 and k2 = 0.01 s–1, with E1 = 10
kcal/mol and E2 = 20 kcal/mol?
Example 8-4
The reactions discussed in Example 8-3 are now to be carried out in a CSTR.
A →k1BB →k2C
1. Determine the exit concentrations from the CSTR.
2. Find the value of the space time τ that will maximize the concentration of B.
e. Example 8-5: LEP Multiple Gas-Phase Reactions in a PBR
Wolfram and Python
1. Vary CT0 from its minimum value to its maximum value and then describe what happens to conversion, selectivity, and molar flow rates.
2. Describe how varying k and CT0 affect the selectivity, SC/D, and the yields, YC and YD.
3. Write a set of conclusions about your experiment in (i) and (ii) above.
Polymath
4. Make slight modifications in the Polymath program to explore the case when the first reaction is reversible
A + 2B←→C
with KC = 0.002 (dm3/mol)2. Compare with the original problem and describe the difference you observe. Vary the ratio of entering flow rates of A to B to learn the effect on selectivity, and then do the same by varying the same for volumetric flow rate.
Example 8-5
The following solid catalyzed complex gas-phase reactions follow elementary rate laws
(1)A+2B→C−r1A′=k1ACACB2(2)2A+3C→D−r2C′=k2CCA2CC3
and take place isothermally in a PBR. The feed is equimolar in A and B with FA0 = 10 mol/min and the volumetric flow rate is 100 dm3/min. The catalyst weight is 1000 kg, the pressure drop is α = 0.0019 kg–1, and the total entering concentration is CT0 = 0.2 mol/dm3.
k1A=100(dm9mol2·kg−cat·min)and k2C=1,500(dm15mol4·kg−cat·min) Plot and analyze FA, FB, FC, FD, p, and SC/D as a function of catalyst weight, W.
f. Example 8-6: LEP Complex Reactions in a Liquid-Phase CSTR
Wolfram and Python
Explore the problem and describe what you find—that is, which parameters have the greatest effects on selectivity.
Example 8-6
The complex reactions discussed in Example 8-5 now take place in the liquid phase in a 2500 dm3 CSTR. The feed is equimolar in A and B with FA0 = 200 mol/min and the volumetric flow rate is 100 dm3/min. The rate constants are k1A=10(dm3mol)2/minandk2c=15(dm3mol)4/min
A + 2B → C
2A + 3 → D
g. Example 8-7: LEP Complex Reactions in a Semibatch Reactor
Wolfram and Python
1. Vary FA0 between its minimum and maximum values and then describe what happens to the profiles when compared to the base case.
2. Which parameter has the greatest effect on selectivity?
3. Write a set of conclusions about your experiments in (i) and (ii) above.
Example 8-7
The complex liquid-phase reactions discussed in Example 8-6 now take place in a semibatch reactor where A is fed to B with FA0 = 3 mol/min. The volumetric flow rate is 10 dm3/min and the initial reactor volume is 1000 dm3. The rate constants are k1A=10(dm3mol)2/minandk2c=15(dm3mol)4/min
A + 2B → C
2A + 3 → D
The maximum volume is 2000 dm3. The inlet concentration of A is CA0 = 0.3 mol/dm3 and the initial concentration of B is CBi = 0.2 mol/dm3.
(a) Plot and analyze NA, NB, NC, ND, and SC/D as a function of time.
8. Example 8-8: LEP Membrane Reactor to Improve Selectivity
Wolfram and Python
A Stop and Smell the Roses Simulation. Play with this simulation to understand the interaction between maximum selectivity and conversion.
1. Vary CT0, k1A, and k2A between their minimum and maximum values to describe what happens to the profiles of the molar flow rates and to the selectivity and conversion.
2. Write a set of conclusions about your experiment in (i) above.
Polymath
3. Describe how your answers would change for the base case if FA0 = 2FA0. What if the reaction were A + 2B → D with the rate law remaining the same? Vary the parameters and describe what you find.
Example 8-8
The reactions
(1) A+B→D−r1A=k1ACA2CB,k1A=2dm6/mol2⋅s(2) A + B→U−r2A=k2ACACB2,k2A=3dm6/mol2⋅s
take place in the gas phase. The overall selectivities, S˜D/U, are to be compared for a membrane reactor (MR) and a conventional PFR. First, we use the instantaneous selectivity to determine which species should be fed through the membrane
SD/U=k1CA2CBk2CB2CA=k1CAk2CB
Prof. Dr. Sven Köttlov in the chemical engineering department at Jofostan University in RiÕa, Jofostan, is one of the best membrane analysts in that area of the world. We see that to maximize SD/U, we need to keep the concentration of A high and the concentration of B low; therefore, we feed small amounts of B along the reactor through the membrane. The molar flow rate of A entering the reactor is 4 mol/s and that of B entering through the membrane is 4 mol/s, as shown in Figure E8-8.1. For the PFR, B enters along with A.
Membrane reactor with one reactant fed through the sides.
A membrane reactor is shown, whose side frames are marked as B and arrows from them are pointed inward, to the reactor. An arrow marked A, representing the reactant, enters the reactor from the left. The frame of the reactor is shown separately, where P subscript s is marked on top and P subscript t at the bottom. An arrow representing v subscript m is drawn across the frame, perpendicular to it. This is marked as C subscript B0. The reactor volume is 50 dm3 and the entering total concentration is 0.8 mol/dm3.
Plot and analyze the molar flow rates and the overall selectivity, S˜D/U, as a function of reactor volume for both the MR and PFR.
i. AspenTech Benzene Pyrolysis Example.
(1) Change the activation energies to E1 = 28 kcal/mol and E2 = 32 kcal/mol, run the AspenTech program, and describe what you find. Compare with original data.
(2) Repeat (1) by changing E1 = 32 kcal/mol and E2 = 28 kcal/mol, and describe what you find.
(3) Double the reactor volume and compare the molar flow rate profiles. Describe what you find.
j. Web Example. PFR Mesitylene Reaction. Download the Living Example Problem (LEP) from the CRE Web site.
(1) How would your answers change if the feed were equal molar in hydrogen and mesitylene?
(2) What is the effect of ΘH on τopt? S˜X/T?
k. Web Example. CSTR Mesitylene Reaction.
l. Read Solved Blood-Coagulation Problem. Download the Living Example Problem.
(1) If blood was flowing out of a small wound at a rate of 0.05 dm3/minute, what is the value of k1 below which would cause you to bleed to death?
(2) Plot out some of the other concentrations, such as TF-VIIa and TF-VIIaX.
(3) Why do the curves look the way they do? What reaction in the cascade is most likely to be inhibited causing one to bleed to death? (4) What reactions, if eliminated, could cause one to die of a blood clot? Hint: Look at ATIIII and/or TFPI.
Step by Step Answer:
a Example 81 i Selectivity increases with an increase in k 2 and decrease in k 1 and k 3 for both PFR and CSTR It is obvious after seeing the expression for selectivity below iv PFR Pressure increased ...View the full answer
