In the summer of 2009, ExxonMobil decided to invest 600 million dollars on developing algae as an alternative fuel and their TV
commercials on this initiative were recently shown (e.g., December 2019). Algae would be grown and their oil extracted to provide an energy source. It is estimated that one acre of a biomass pond can provide 6000 gal of gasoline per year, which would require the capture of a CO2 source more concentrated than air (e.g., fuel gas from a refinery) and also contribute to the sequestration of CO₂. The biomass biosynthesis during the day is The contributions of John Benemann to this problem are appreciated.
Sunlight + CO₂ + H₂O + Algae → More Algae + O₂
Consider a 5000-gal pond with perforated pipes into which CO₂ is injected and slowly bubbled into the solution to keep the water saturated with CO₂.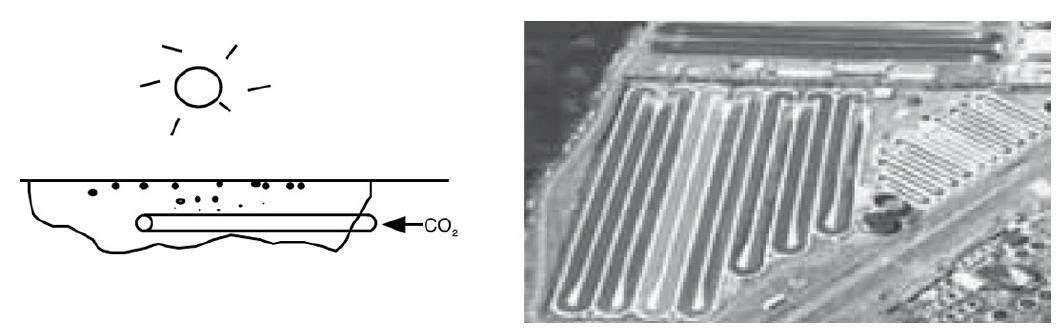

An illustration and a photograph depicting microalgae production are shown. The illustration depicts Carbon di Oxide supplied to a pond, where microalgae production is initiated. Carbon di Oxide is supplied through perforated pipes and the sunlight also helps in the production of more algae. A photograph of an open raceway pond is shown. Microalgae production is already initiated in the raceway and the raceway pond is paddle-wheel driven. The doubling time during the day is 12 h at high-noon sunlight and zero during the night. As a first approximation, the growth during the 12 hours of daylight law is r_g = fμC_C with f = sunlight = sin (πt/12) between 6 A.M. and 6 P.M., otherwise f = 0, C_C is the algae concentration (g/dm³) and μ = 0.9 day^–1 (assumes constant CO₂ saturation at 1 atm is 1.69 g/kg water). The pond is 30-cm deep and for effective sunlight penetration, the algae concentration cannot exceed 200 mg/dm³.

a. Derive an equation for the ratio of the algae cell concentration C_C at time t to initial cell concentration C_C0, that is, (C_C/C_C0). Plot and analyze (C_C/C_C0) versus time up to 48 hours.

b. If the pond is initially seeded with 0.5 mg/dm³ of algae, how long will it take the algae to reach a cell density (i.e., concentration) of 200 mg/dm³, which is the concentration at which sunlight can no longer effectively penetrate the depth of the pond? Plot and analyze r_g and C_C as a function of time. As a first approximation, assume the pond is well mixed.

c. Suppose the algae limit the sun’s penetration significantly even before the concentration reaches 200 mg/dm³ with, for example, μ = μ₀ (1 – C_C/200). Plot and analyze r_g and C_C as a function of time. How long would it take to completely stop growth at 200 mg/dm³?

d. Now, let’s consider continuous operation. Once the cell density reaches 200 mg/dm, one-half of the pond is harvested and the remaining broth is mixed with fresh nutrient. What is the steady-state algae productivity in gm/year, again assuming the pond is well mixed?

e. Now consider a constant feed of waste water and removal of algae at a dilution rate of one reciprocal day. What is the mass flow rate of algae out of the 5000-gal pond (g/d)? Assume the pond is well mixed.

f. Now consider that the reaction is to be carried out in an enclosed, transparent reactor. The reactor can be pressurized with CO₂ up to 10 atm with KS = 2 g/dm³.
Assume that after the initial pressurization, no more CO₂ can be injected. Plot and analyze the algae concentration as a function of time.
g. An invading algae can double twice as fast as the strain you are cultivating. Assume that it initially is at 0.1 mg/l concentration. How long until it is the dominant species (over 50% of the cell density)?

Transcribed Image Text:

CO