At rush hours, substantial traffic congestion is encountered at the traffic intersections shown in the figure. (All
Question:
At rush hours, substantial traffic congestion is encountered at the traffic intersections shown in the figure. (All streets are one-way.) The city wishes to improve the signals at these corners to speed the flow of traffic. The traffic engineers first gather data. As the figure shows, 700 cars per hour come down M Street to intersection A, and 300 cars per hour come to intersection A on 10th Street. A total of x1 of these cars leave A on M Street, while x4 cars leave A on 10th Street. The number of cars entering A must equal the number leaving, which suggests the following equation.
x1 + x4 = 700 + 300
x1 + x4 = 1000
For intersection B, x1 cars enter B on M Street, and x2 cars enter B on 11th Street. As the figure shows, 900 cars leave B on 11th Street, while 200 leave on M Street, which leads to the following equation.
x1 + x2 = 900 + 200
x1 + x2 = 1100
At intersection C, 400 cars enter on N Street and 300 on 11th Street, while x2 cars leave on 11th Street and x3 cars leave on N Street.
x2 + x3 = 400 + 300
x2 + x3 = 700
Finally, intersection D has x3 cars entering on N Street and x4 cars entering on 10th Street. There are 400 cars leaving D on 10th Street and 200 leaving on N Street.
(a) Set up an equation for intersection D.
(b) Use the four equations to write an augmented matrix, and then transform it so that 1s are on the diagonal and 0s are below. This is triangular form.
(c) Since there is a row of all 0s, the system of equations does not have a unique solution. Write three equations, corresponding to the three nonzero rows of the matrix. Solve each of the equations for x4.
(d) One of the equations should have been x4 = 1000 - x1. What is the greatest possible value of x1 so that x4 is not negative?
(e) Another equation should have been x4 = x2 - 100. Find the least possible value of x2 so that x4 is not negative.
(f) Find the greatest possible values of x3 and x4 so that neither variable is negative.
(g) Use the results of parts (a)–(f) to give a solution for the problem in which all the equations are satisfied and all variables are nonnegative. Is the solution unique?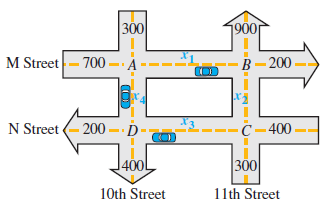
Step by Step Answer:

College Algebra
ISBN: 978-0134697024
12th edition
Authors: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels





