(a) How long does it take the astronaut in Example 28.2 to travel 4.30 ly at 0.99944c (as measured by the Earth-bound observer)?

(b) How long does it take according to the astronaut? 

(c) Verify that these two times are related through time dilation with γ=30.00 as given.

Data from Example 28.2

Suppose an astronaut, such as the twin discussed in Simultaneity and Time Dilation, travels so fast that γ=30.00 .

(a) She travels from the Earth to the nearest star system, Alpha Centauri, 4.300 light years (ly) away as measured by an Earth-bound observer. How far apart are the Earth and Alpha Centauri as measured by the astronaut?

(b) In terms of c, what is her velocity relative to the Earth? You may neglect the motion of the Earth relative to the Sun. (See Figure 28.11.)

Strategy

First note that a light year (ly) is a convenient unit of distance on an astronomical scale-it is the distance light travels in a year. For part (a), note that the 4.300 ly distance between the Alpha Centauri and the Earth is the proper distance L₀, because it is measured by an Earth-bound observer to whom both bodies are (approximately) stationary. To the astronaut, the Earth and the Alpha Centauri are moving by at the same velocity, and so the distance between them is the contracted length L. In part (b), we are given y, and so we can find v by rearranging the definition of γ to express v in terms of c.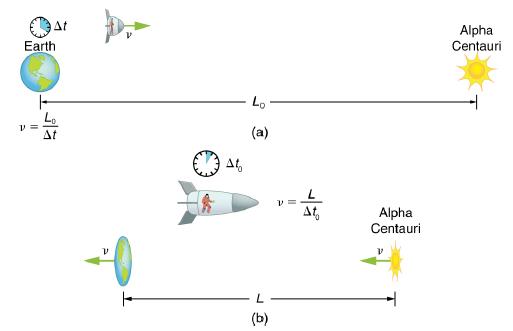

At Earth At V At, Lo (a) JB (b) V= L At Alpha Centauri Alpha Centauri