(a) What are the three smallest thicknesses of a soap bubble that produce constructive interference for red light with a wavelength of 650 nm? The index of refraction of soap is taken to be the same as that of water. 

(b) What three smallest thicknesses will give destructive interference?

Strategy and Concept

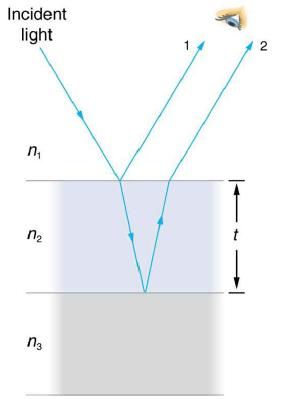
Use Figure 27.33 to visualize the bubble. Note that n₁ = n₃ = 1.00 for air, and n₂ = 1.333 for soap (equivalent to water). There is a λ/2 shift for ray 1 reflected from the top surface of the bubble, and no shift for ray 2 reflected from the bottom surface. To get constructive interference, then, the path length difference (2t) must be a half-integral multiple of the wavelength-the first three being λ_n/2, 3λ_n/2, and 5λ_n/2. To get destructive interference, the path length difference must be an integral multiple of the wavelength-the first three being 0, λ_n, and 2λ_n).

Data from figure 27.33

Transcribed Image Text:

Incident light n₁ n₂ n3 1 2