In Example 7.7, we calculated the final speed of a roller coaster that descended 20 m in height and had an initial speed of 5 m/s downhill. Suppose the roller coaster had had an initial speed of 5 m/s uphill instead, and it coasted uphill, stopped, and then rolled back down to a final point 20 m below the start. We would find in that case that its final speed is the same as its initial speed. Explain in terms of conservation of energy.

Data given in Example 7.7

(a) What is the final speed of the roller coaster shown in Figure 7.8 if it starts from rest at the top of the 20.0 m hill and work done by frictional forces is negligible?

(b) What is its final speed (again assuming negligible friction) if its initial speed is 5.00 m/s?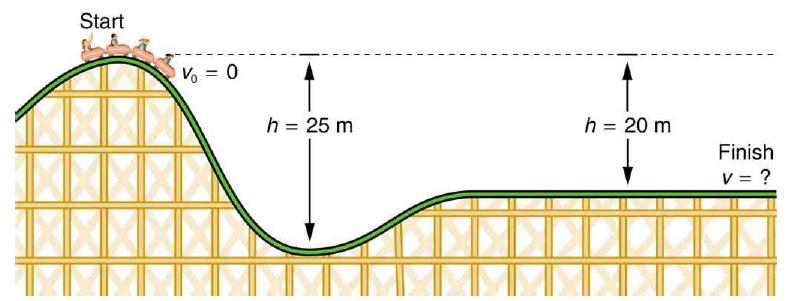

Strategy

The roller coaster loses potential energy as it goes downhill. We neglect friction, so that the remaining force exerted by the track is the normal force, which is perpendicular to the direction of motion and does no work. The net work on the roller coaster is then done by gravity alone. The loss of gravitational potential energy from moving downward through a distance equals the gain in kinetic energy. This can be written in equation form as Using the equations for PE_g and KE, we can solve for the final speed v, which is the desired quantity.

Transcribed Image Text:

Start V = 0 h = 25 m h = 20 m Finish V = ?