This problem returns to the tightrope walker studied in Example 4.6, who created a tension of 3.94 x 10³ N in a wire making an angle 5.0° below the horizontal with each supporting pole. Calculate how much this tension stretches the steel wire if it was originally 15 m long and 0.50 cm in diameter.

Data given in Example 4.6

Calculate the tension in the wire supporting the 70.0-kg tightrope walker shown in Figure 4.16.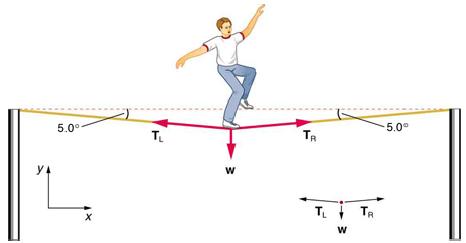

Strategy

As you can see in the figure, the wire is not perfectly horizontal (it cannot be!), but is bent under the person`s weight. Thus, the tension on either side of the person has an upward component that can support his weight. As usual, forces are vectors represented pictorially by arrows having the same directions as the forces and lengths proportional to their magnitudes. The system is the tightrope walker, and the only external forces acting on him are his weight w and the two tensions T_L (left tension) and T_R (right tension), as illustrated. It is reasonable to neglect the weight of the wire itself. The net external force is zero since the system is stationary. A little trigonometry can now be used to find the tensions. One conclusion is possible at the outset-we can see from part (b) of the figure that the magnitudes of the tensions T_L and T_R must be equal. This is because there is no horizontal acceleration in the rope, and the only forces acting to the left and right are T_L and T_R. Thus, the magnitude of those forces must be equal so that they cancel each other out.

Whenever we have two-dimensional vector problems in which no two vectors are parallel, the easiest method of solution is to pick a convenient coordinate system and project the vectors onto its axes. In this case the best coordinate system has one axis horizontal and the other vertical. We call the horizontal the -axis and the vertical the -axis.

Transcribed Image Text:

YA 5.0⁰- X TL W TR T₁ W TR -5.0°