A cylindrical tank containing water has a small hole punched in its side below the water level,
Question:
A cylindrical tank containing water has a small hole punched in its side below the water level, and water runs out (Figure 9.21). What is the approximate initial flow rate of water out of the tank in terms of the heights shown?
THINKING IT THROUGH. Equation \(9.17\left(A_{1} v_{2}=A_{2} v_{2}\right)\) is the flow rate equation, where \(A v\) has units of \(\mathrm{m}^{3} / \mathrm{s}\), or volume/time. The \(v\) terms can be related by Bernoulli's equation, which also contains \(y\), and can be used to find differences in height. The areas are not given, so relating the \(v\) terms might require some sort of approximation, as will be seen. (Note that the approximate initial flow rate is wanted.) 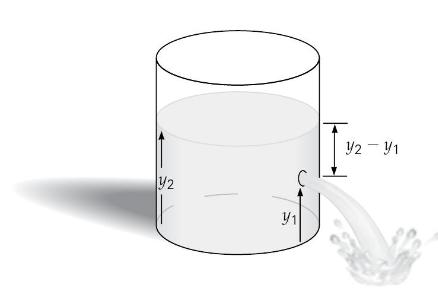
Step by Step Answer:

College Physics Essentials Electricity And Magnetism Optics Modern Physics Volume Two
ISBN: 9781032337272
8th Edition
Authors: Jerry D. Wilson, Anthony J. Buffa, Bo Lou





