Suppose that two masses, \(m_{1}=2.5 \mathrm{~kg}\) and \(m_{2}=3.5 \mathrm{~kg}\), are connected by light strings and are in uniform circular motion on a horizontal frictionless surface as illustrated in Figure 7.13, where \(r_{1}=1.0 \mathrm{~m}\) and \(r_{2}=1.3 \mathrm{~m}\). The tension forces acting on the masses are \(T_{1}=4.5 \mathrm{~N}\) and \(T_{2}=2.9 \mathrm{~N}\), which are the respective tensions in the strings. Find the magnitude of the centripetal acceleration and the tangential speed of

(a) mass \(m_{2}\) and

(b) mass \(m_{1}\).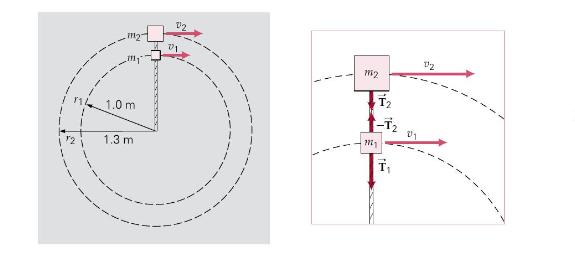

THINKING IT THROUGH. The centripetal forces on the masses are supplied by the tensions ( \(T_{1}\) and \(T_{2}\) ) in the strings. By isolating the masses, \(a_{c}\) for each mass can be found, because the net force on a mass is equal to the mass's centripetal force \(\left(F_{\mathrm{c}}=m a_{c}\right)\). The tangential speeds can then be found, since the radii are known \(\left(a_{c}=v^{2} / r\right)\) 

Transcribed Image Text:

1.0 m 12 1.3 m 01 12 132 1-12 1 01