The femur (upper leg bone) is the longest and strongest bone in the body. Taking a typical
Question:
The femur (upper leg bone) is the longest and strongest bone in the body. Taking a typical femur to be approximately circular in cross-section with a radius of \(2.0 \mathrm{~cm}\), how much force would be required to extend a patient's femur by \(0.010 \%\) while in horizontal traction?
THINKING IT THROUGH. Equation 9.4 should apply, but where does the percentage increase fit in? This question can be answered as soon as it is recognized that the \(\Delta L / L_{\mathrm{o}}\) term is the fractional increase in length. For example, if you had a spring with a length of \(10 \mathrm{~cm}\left(L_{\mathrm{o}}\right)\) and you stretched it \(1.0 \mathrm{~cm}(\Delta L)\), then \(\Delta L / L_{\mathrm{o}}=1.0 \mathrm{~cm} / 10 \mathrm{~cm}=0.10\). This ratio can readily be changed to a percentage, and the spring's length was increased by \(10 \%\). So the percentage increase is really just the value of the \(\Delta L / L_{\mathrm{o}}\) term (multiplied by \(100 \%\) ). Equation (9.4): 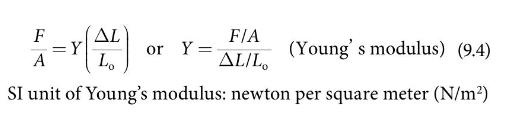
Step by Step Answer:

College Physics Essentials Electricity And Magnetism Optics Modern Physics Volume Two
ISBN: 9781032337272
8th Edition
Authors: Jerry D. Wilson, Anthony J. Buffa, Bo Lou





