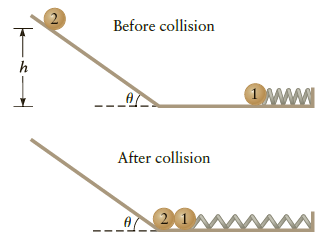
A mass of 3.5 kg is attached to a spring with spring constant k = 70 N/m. It is then compressed by 49 cm from its equilibrium position (Fig. P11.67, top) and released. At exactly the same time, an identical mass is released down a friction less slope inclined at angle θ = 40^o from the horizontal, and the two masses collide when this mass reaches the bottom of the slope (Fig. P11.67, bottom). At the moment the two masses collide, the spring is neither stretched nor compressed. The system is designed to produce periodic motion for both masses such that they always end up colliding at the same position. Assume there is no friction in the system and the collision is perfectly elastic. 

(a) What is the period of this oscillating system? 

(b) From what height h must the second mass be released so that it will collide with the mass on the spring? Consider the period of motion of the first mass and the acceleration of the second mass in determining the needed release point up the slope. 

(c) Sketch the first 2.0 s of the displacement– time graph for the horizontal (x) displacement of the first mass. On the same axes, draw the displacement–time graph for the vertical (y) displacement of the second mass.

Figure P11.67

 

Transcribed Image Text:

Before collision After collision