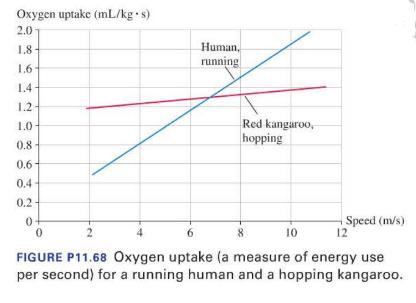
At approximately what speed would a human use half the power of an equal-mass kangaroo moving at the same speed?

A. \(3 \mathrm{~m} / \mathrm{s}\)

B. \(4 \mathrm{~m} / \mathrm{s} \quad\) C. \(5 \mathrm{~m} / \mathrm{s}\)

D. \(6 \mathrm{~m} / \mathrm{s}\)

Kangaroos have very stout tendons in their legs that can be used to store energy. When a kangaroo lands on its feet, the tendons stretch, transforming kinetic energy of motion to elastic potential energy. Much of this energy can be transformed back into kinetic energy as the kangaroo takes another hop. The kangaroo's peculiar hopping gait is not very efficient at low speeds but is quite efficient at high speeds. Figure P11.68 shows the energy cost of human and kangaroo locomotion. The graph shows oxygen uptake (in \(\mathrm{mL} / \mathrm{s}\) ) per \(\mathrm{kg}\) of body mass, allowing a direct comparison between the two species.
For humans, the energy used per second (i.e., power) is proportional to the speed. That is, the human curve nearly passes through the origin, so running twice as fast takes approximately twice as much power. For a hopping kangaroo, the graph of energy use has only a very small slope. In other words, the energy used per second changes very little with speed. Going faster requires very little additional power. Treadmill tests on kangaroos and observations in the wild have shown that they do not become winded at any speed at which they are able to hop. No matter how fast they hop, the necessary power is approximately the same.