If the (mathrm{C}) were played on an organ pipe that was open at one end and closed
Question:
If the \(\mathrm{C}\) were played on an organ pipe that was open at one end and closed at the other, which of the harmonic frequencies in Figure P16.70 would be present?
A. All of the harmonics in the figure would be present.
B. 262,786 , and \(1310 \mathrm{~Hz}\)
C. 524,1048 , and \(1572 \mathrm{~Hz}\)
D. 262,524 , and \(1048 \mathrm{~Hz}\)
You know that certain musical notes sound good togetherharmonious-whereas others do not. This harmony is related to the various harmonics of the notes.
The musical notes \(\mathrm{C}(262 \mathrm{~Hz})\) and G (392 Hz) make a pleasant sound when played together; we call this consonance. As Figure P16.70 shows, the harmonics of the two notes are either far from each other or very close to each other (within a few \(\mathrm{Hz}\) ). This is the key to consonance: harmonics that are spaced either far apart or very close. The close harmonics have a beat frequency of a few Hz that is perceived as pleasant. If the harmonics of two notes are close but not too close, the rather high beat frequency between the two is quite unpleasant. This is what we hear as dissonance. Exactly how much a difference is maximally dissonant is a matter of opinion, but harmonic separations of 30 or \(40 \mathrm{~Hz}\) seem to be quite unpleasant for most people.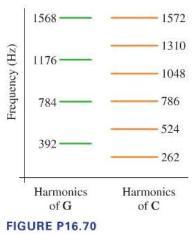
Step by Step Answer:

College Physics A Strategic Approach
ISBN: 9780321907240
3rd Edition
Authors: Randall D. Knight, Brian Jones, Stuart Field





