If the top (500 mathrm{~m}) of ocean water increased in temperature from (17^{circ} mathrm{C}) to (18^{circ} mathrm{C}),
Question:
If the top \(500 \mathrm{~m}\) of ocean water increased in temperature from \(17^{\circ} \mathrm{C}\) to \(18^{\circ} \mathrm{C}\), what would be the resulting rise in ocean height?
A. \(0.11 \mathrm{~m}\)
B. \(0.22 \mathrm{~m}\)
C. \(0.44 \mathrm{~m}\)
D. \(0.88 \mathrm{~m}\)
Seasonal temperature changes in the ocean only affect the top layer of water, to a depth of \(500 \mathrm{~m}\) or so. This "mixed" layer is thermally isolated from the cold, deep water below. The average temperature of this top layer of the world's oceans, which has area \(3.6 \times 10^{8} \mathrm{~km}^{2}\), is approximately \(17^{\circ} \mathrm{C}\). In addition to seasonal temperature changes, the oceans have experienced an overall warming trend over the last century that is expected to continue as the earth's climate changes. A warmer ocean means a larger volume of water; the oceans will rise. Suppose the average temperature of the top layer of the world's oceans were to increase from a temperature \(T_{\mathrm{i}}\) to a temperature \(T_{\mathrm{f}}\). The area of the oceans will not change, as this is fixed by the size of the ocean basin, so any thermal expansion of the water will cause the water level to rise, as shown in Figure P12.109. The original volume is the product of the original depth and the surface area, \(V_{\mathrm{i}}=A d_{\mathrm{i}}\). The change in volume is given by \(\Delta V=A \Delta d\).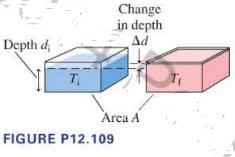
Step by Step Answer:

College Physics A Strategic Approach
ISBN: 9780321907240
3rd Edition
Authors: Randall D. Knight, Brian Jones, Stuart Field





