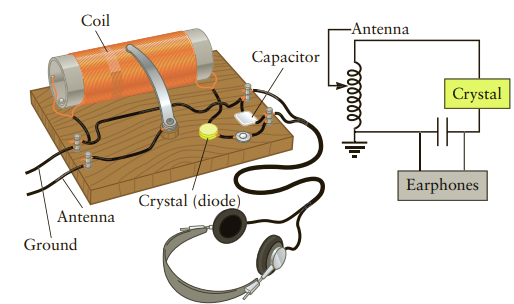
The phenomenon of resonance makes it possible to listen to AM broadcasts with a very simple circuit and never need a battery. When a system is driven at its resonant frequency, even if by minute oscillations of current in the antenna, the resulting amplitude can be many times greater than the driving amplitude. The crystal radio, when tuned to a broadcast frequency, can produce a current large enough to operate an earphone speaker. A crystal radio is a simple LCR circuit with an antenna wire and a diode (the “crystal,” involved in separating the signal from the carrier wave for the earphone). Figure P22.83 shows an illustration and circuit diagram of such a radio. The LCR circuit is made to match the broadcast frequency by varying the inductance, in this case by moving a wire to select how many turns of the solenoid are included in the circuit.
(a) If the capacitance of the circuit is 950 pF, what inductance is needed to receive a broadcast at the highest AM frequency (1710 kHz)? At the lowest (520 kHz)?
(b) The solenoid inductor’s windings are made on a cylinder 6.0 cm in diameter and 20 cm long. How many turns are needed to provide the maximum and minimum inductances to cover the full AM band range?
(c) Calculate the number of windings per length of solenoid (turns per millimeter). 

(d) AM radio specifications mandate that stations are spaced 10 kHz apart. Will this solenoid have sufficient resolution to separate two stations? (What change in the resonant frequency is produced by including one more winding?)

Transcribed Image Text:

Coil -Antenna Capacitor Crystal Earphones Crystal (diode) Antenna Ground