What is the angular acceleration of the anther sac during the motion? A. (3.5 times 10^{3} mathrm{rad}
Question:
What is the angular acceleration of the anther sac during the motion?
A. \(3.5 \times 10^{3} \mathrm{rad} / \mathrm{s}^{2}\)
B. \(7.0 \times 10^{3} \mathrm{rad} / \mathrm{s}^{2}\)
C. \(1.2 \times 10^{7} \mathrm{rad} / \mathrm{s}^{2}\)
D. \(2.3 \times 10^{7} \mathrm{rad} / \mathrm{s}^{2}\)
The bunchberry flower has the fastest-moving parts ever seen in a plant. Initially, the stamens are held by the petals in a bent position, storing energy like a coiled spring. As the petals release, the tips of the stamens fly up and quickly release a burst of pollen. Figure P7.72 shows the details of the motion. The tips of the stamens act like a catapult, flipping through a \(60^{\circ}\) angle; the times on the earlier photos show that this happens in just \(0.30 \mathrm{~ms}\). We can model a stamen tip as a \(1.0-\mathrm{mm}\)-long, \(10 \mu \mathrm{g}\) rigid rod with a \(10 \mu \mathrm{g}\) anther sac at one end and a pivot point at the opposite end. Though an oversimplification, we will model the motion by assuming the angular acceleration is constant throughout the motion.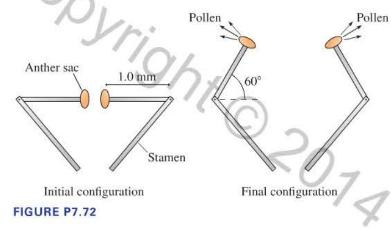
Step by Step Answer:

College Physics A Strategic Approach
ISBN: 9780321907240
3rd Edition
Authors: Randall D. Knight, Brian Jones, Stuart Field





