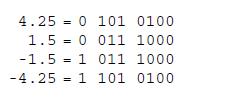
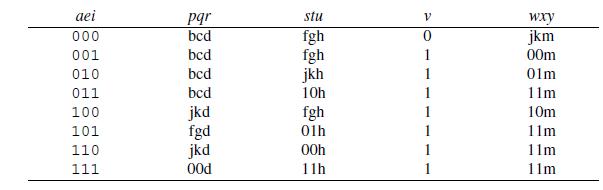
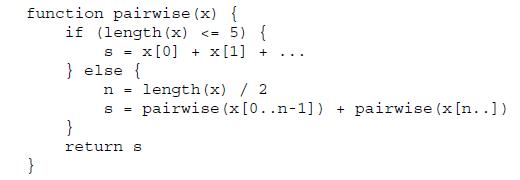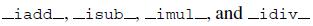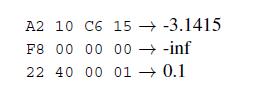Numbers And Computers 1st Edition Ronald T Kneusel - Solutions

Discover comprehensive resources for "Numbers And Computers 1st Edition" by Ronald T Kneusel. Access online answers key and solutions pdf for solved problems, providing step-by-step answers to enhance your understanding. Our solution manual and instructor manual offer detailed chapter solutions and a valuable test bank to support your learning journey. Whether you're looking for questions and answers or need a textbook guide, our free download ensures you have all the tools necessary for success. Unlock the full potential of this textbook with our expertly crafted resources.

Using Egyptian notation and method calculate 22 × 48 and 713 ÷ 31.
Using Babylonian notation calculate 405 + 768.
Using Mayan notation calculate 419+2105. (Hint: carry on twenty, not ten)
Convert the following hexadecimal numbers to binary: A9C116, 20ED16, FD6016.
Convert the following octal numbers to binary: 7738, 2038, 6568.
Using the table method, convert 6502 to binary.
Using the division method, convert 8008 to binary.
Write e = 2.71828182845904. . . to at least four decimal places using Babylonian notation.
Write a program to convert a number in any base < 37 to its decimal equivalent using the recurrence relation. Use a string to hold the number itself and use 0−9 and capital letters A−Z for the digits.
Interpret the following bit patterns first as little-endian then as big-endian unsigned short integers. Convert your answer to decimal.• 1101011100101110• 1101010101100101• 0010101011010101• 1010101011010111
Given A = 6B16 and B = D616, write the result of each expression in binary and hexadecimal.• (A AND B) OR (NOT A)• (A XOR B) OR (A AND (NOT B))• ((NOT A) OR (NOT B)) XOR (A AND B)
Using C syntax write an expression that achieves each of the following. Assume that the unsigned char A = 0x8A.• Set bits 3 and 6 of A.• Keep only the low nibble of A.• Set unsigned char B to 100 if bit 3 of A is not set.• Clear bit 1 of A.• Toggle bits 4 and 5 of A.
Using C syntax write an expression for each of the following.• Swap the upper and lower nibbles of unsigned char v = 0xC4.• Multiply v by 5 using at least one shift operation.
Express each of the following numbers in one’s and two’s complement notation.Write your answer in binary and hexadecimal. Assume 8-bit signed integers.• −14• −127• −1
Write a function to reverse the bits of an unsigned 8-bit integer.
Write a function to count the number of 1 bits in an unsigned 32-bit integer.
The Hamming distance between two integers is the number of places where their corresponding bits differ. For example, the Hamming distance between 1011 and 0010 is 2 because the numbers differ in bits 0 and 3. Write a function to calculate the Hamming distance between two unsigned short integers.
A Gray code is a sequence of bit patterns in which any two adjacent patterns in the sequence differ by only one bit. Gray codes were developed to aid in error correction of mechanical switches but are used more generally in digital systems. For example, for four bits, the first six values in the
Convert the following 32-bit IEEE bit patterns to their corresponding floatingpoint values:(a) 0 10000000 10010010000111111011011(b) 0 10000000 01011011111100001010100(c) 0 01111111 10011110001101110111101(d) 0 01111110 01100010111001000011000(e) 0 01111111 01101010000010011110011 Where the first
Assume a simple floating-point representation that uses four bits in the significand, three bits for the exponent, and one for the sign. The exponent is stored in excess-3 format and all exponent values are valid. In this case we have the following representations,Work out the following sums and
Modify fp compare to handle infinities properly.
Summing the values of an array is a common operation. If the naive implementation is used, simply adding each new array element to the accumulated sum of all the previous, there will be an overall round-off error proportional to the number of terms added. For a small array this is negligible but
Big integer libraries typically represent integers in sign-magnitude format as we did in this chapter. Another possibility would be to use a complement notation, call it B’s-complement where B is the base, which is the analog of 2’s-complement used almost exclusively for fixed-length integers.
We gave a C function for bigint_equal to test if two big integers are equal. This function made use of bigint_compare. Write the remaining comparison functions for , ≤, ≥ and ≠.
Figure 4.11 implements a function to perform big integer division. Extend this function to return the remainder as well. 1 signed int bigint_udiv (signed int *a, signed int *b) { signed int *q, *t, *c, x=NULL, *y=NULL; 2 q (signed int *)malloc(2* sizeof (signed int)); q[0] = 1; c (signed int
Add a new function to our library, bigint_pow(a,b), which returns ab. Be sure to handle signs and special cases.
Add another new function to our library, bigint_fact(a), which returns a!. Recall that the argument must be ≥ 0.
Using the big integer functions defined in this chapter create a simple arbitrary precision desk calculator in C which takes as input expressions of the form “A op B”, as a string, where A and B are big integers and op is one of the four basic arithmetic operations and returns the result. If
Extend the basic Rational Python class outlined above to compare rational numbers by overriding theand ne methods to implement comparison operators , ≥, ==, and ≠. _lt_, _le_, _gt_, _ge_, _eq_, and _ne_
Extend the basic Rational Python class outlined above by adding _neg_, _abs_ methods for negation and absolute value.
Extend the basic Rational Python class outlined above by adding methods to handle shortcut operations. N.B., these, unlike all the others, destructively update the existing rational object. They do not return a new object. The method names are: corresponding to operators +=, –=, *=, and /=. Be
Use the Rational class to create a simple interactive rational desk calculator. This should take as input expressions of the form “A op B”, as a string, where A and B are rationals (with a “/” character) or integers and op is one of the four basic arithmetic operations and return the
The function Q_sin_table rounds its argument to the nearest degree and then returns the sine stored in the precomputed table for that degree. This can be made more accurate by linearly interpolating between the degrees that bound the input angle. For example, if the input value, as a fixed-point
Add a function, Q_ipow, to the library that takes two arguments. The first is a fixed-point number, \(x\), and the second is an integer, \(n\), which may be negative. The return value of the function is \(x^{n}\).
Add a function, Q_pow, to the library that takes two arguments. The first is a fixed-point number, \(x\), and the second is also a fixed-point number, \(y\). The return value of the function is \(x^{y}\). ( \(x^{y}=e^{y \log (x)}\) )
Add a function, Q_asin, to the library that takes a sine value, positive and negative, and returns the angle for that sign, in radians. Use a Taylor series expansion,\[ \sin ^{-1}
Create a Python class, Fixed, that duplicates the arithmetic functionality of the C fixed-point library. Be sure to overload the operators for,,\(+- /, *\) so that the fixed-point class can be used in expressions.
The function Q_sin_taylor uses terms out to \(x^{9}\) and calculates them explicitly for input \(x\). Show via algebraic manipulation that the same truncated series sum can be found using only \(x\) and \(x^{2}\). Then, update Q_sin_taylor to use this form. Note that you will need to introduce new
Parse the following decimal64 numbers: 29 ff 98 42 d2 e9 64 45 25 ff 18 Oc ce ef 26 1f 25 fe 14 44 ee 27 cc 5b.
The function dfp parse() in Fig. 6.1 works with decimal64 numbers only. Create a version that works with decimal32 numbers. Test it with the following inputs, A2 10 C6 15 -3.1415 F8 00 00 00 -inf 22 40 00 01 0.1
Encode the number 123.456 as a decimal64 number. First decide on the significand and exponent to use, then encode the exponent and first digit of the significand to create the CF and BXCF fields. Last, use Table 6.3 to encode the significand mapping the remaining 15 decimal digits to five
Add int_lt (), int_gt (), int_ge (), and int_ne () functions to test for \(\), \(\geq\), and \(eq\) using int_eq () and int_le ().
Add exponential \(\left(e^{x}\right)\), square root \((\sqrt{x})\) and logarithm functions (any base) to the \(\mathrm{C}\) interval library.
The Python interval class only contains basic operations. Complete the class by adding the missing operations found in the \(\mathrm{C}\) library.
Extend the Python interval library to support mixed scalar and interval arithmetic for,,\(+- \times\), and /.
Extend the Python _-_pow_-() method to proper handle negative integer exponents.
Extend the \(\mathrm{C}\) library by adding cosine using the formulas in Sect. 7.3.Formulas from Section 7.3 f(x) = ([xx]) = [(x), (x)]
Extend the Python class by adding sine and cosine using the formulas in Sect. 7.3.Formulas from Section 7.3 f(x) = ([xx]) = [(x), (x)]
Add interval splitting to the Python interval class in order to minimize the dependency problem. Automatically split intervals into \(n\) parts and evaluate a function on each of those parts reporting the union of them when complete.

Numbers And Computers 1st Edition Ronald T Kneusel - Solutions

Step by Step Answers