An interval polynomial is of the form

P(s) = a₀ + a₁s + a₂s² + a₃s³ + a₄s⁴ + a₅s⁵ + ∙ ∙ ∙

with its coefficients belonging to intervals x_i ≤ a_i ≤  y_i, where xi, yi are prescribed constants. Kharitonov’s theorem says that an interval polynomial has all its roots in the left half-plane if each one of the following four polynomials has its roots in the left half-plane (Minichelli, 1989):

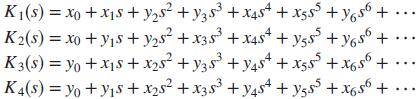
Use Kharitonov’s theorem and the Routh-Hurwitz criterion to find if the  following polynomial has any zeros in the right half-plane.

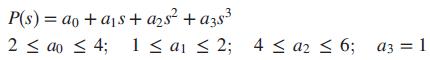
K1(s) = xo +x1s + y,s +y3s + x4s+ + xgs + Y6s6 + K2(s) = xo + y,5s+ y2s +x3s+X4s* + yss + ygs + ... K3(s) = yo + x1s+ x2s + y3s +y4s* + xss + x6s + K4(s) = yo + y1s+ x2s2 +x3s + yast + y,s + x6s6+. %3D