Question: Given the HIV system of Problem 84 in Chapter 4 and repeated here for convenience (Craig, 2004): Express the system in the following forms: a.
Given the HIV system of Problem 84 in Chapter 4 and repeated here for convenience (Craig, 2004):
![-0.04167 0 -0.0058 [T 0.0217 -0.24 0.0058 T* 100 -2.4 5.2] +|](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1610/6/1/7/64060001328573031610617639646.jpg)
Express the system in the following forms:
a. Phase-variable form
b. Controller canonical form
c. Observer canonical form
Finally,
d. Use MATLAB to obtain the system’s diagonalized representation.
Data from Problem 84 in Chapter 4:
We developed a linearized state-space model of HIV infection. The model assumed that two different drugs were used to combat the spread of the HIV virus. Since this book focuses on single-input, single output systems, only one of the two drugs will be considered. We will assume that only RTIs are used as an input. Thus, in the equations of Chapter 3, Problem 31, u2 = 0 (Craig, 2004).
a. Show that when using only RTIs in the linearized system of Problem 31, Chapter 3, and substituting the typical parameter values given in the table of Problem 31c, Chapter 3, the resulting state-space representation for the system is given by
![-5.2 | 1 T y = [0 0 1] T* II](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1610/6/0/6/2345fffe69a6f1491610606235489.jpg)
b. Obtain the transfer function from RTI efficiency to virus count; namely, find Y(s)/U1(s).
c. Assuming RTIs are 100% effective, what will be the steady-state change of virus count in a given infected patient? Express your answer in virus copies per ml of plasma. Approximately how much time will the medicine take to reach its maximum possible effectiveness?
Data from Chapter 3, Problem 31:
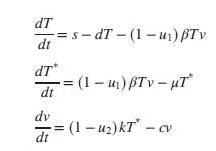
-0.04167 0 -0.0058 [T 0.0217 -0.24 0.0058 T* 100 -2.4 5.2] +| -5.2 | 1 T y = [0 0 1] T* II
Step by Step Solution
3.39 Rating (177 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


