In Chapter 6, the model for an HIV/AIDS patient treated with RTIs was linearized and shown to
Question:
In Chapter 6, the model for an HIV/AIDS patient treated with RTIs was linearized and shown to be
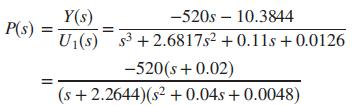
It is assumed here that the patient will be treated and monitored using the closed-loop configuration shown in Figure P11.1 Since the plant has a negative dc gain, assume for simplicity that G(s) = Gc(s) P(s) and Gc(0) < 0. Assume also that the specifications for the design are (1) zero steady-state error for step inputs, (2) overdamped time-domain response, and (3) settling time Ts ≈100 days (Craig, 2004).
a. The overdamped specification requires a ΦM ≈ 90°. Find the corresponding bandwidth required to satisfy the settling time requirement.
b. The zero steady-state error specification implies that the open-loop transfer function must be augmented to Type 1. The -0.02 zero of the plant adds too much phase lead at low frequencies, and the complex conjugate poles, if left uncompensated within the loop, result in undesired oscillations in the time domain. Thus, as an initial approach to compensation for this system we can try
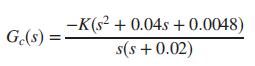
For K = 1, make a Bode plot of the resulting system. Obtain the value of K necessary to achieve the design demands. Check for closed-loop stability.
c. Simulate the unit step response of the system using MATLAB. Adjust K to achieve the desired response.
Step by Step Answer:
This question has not been answered yet.
You can Ask your question!
