Harold and Helen Nash are saving for the college education of their newborn daughter, Susan. The Nashes estimate that college expenses will run $30,000 per year when their daughter reaches college in 18 years. The annual discount rate over the next few decades will be 14 percent. How much money must they deposit in the bank each year so that their daughter will be completely supported through four years of college?

To simplify the calculations, we assume that Susan is born today. Her parents will make the first of her four annual tuition payments on her 18th birthday. They will make equal bank deposits on each of her first 17 birthdays, but no deposit at Year 0. This is illustrated as follows: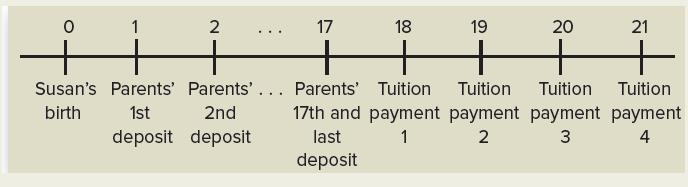

The Nashes will be making deposits to the bank over the next 17 years. They will be withdrawing $30,000 per year over the following four years. We can be sure they will be able to withdraw fully $30,000 per year if the present value of the deposits is equal to the present value of the four withdrawals of $30,000.

This calculation requires three steps. The first two determine the present value of the withdrawals. The final step determines yearly deposits that will have a present value equal to that of the withdrawals.

1. We calculate the present value of the four years at college using the annuity formula: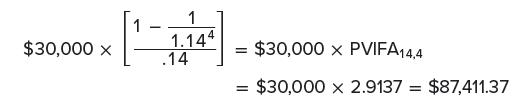

We assume that Susan enters college on her 18th birthday. Given our discussion in Trick 1, $87,411.37 represents the value at Year 17.

2. We calculate the present value of the college education at Year 0 as:

3. Assuming that Harold and Helen Nash make deposits to the bank at the end of each of the 17 years, we calculate the annual deposit that will yield a present value of all deposits of $9,422.92. This is calculated as: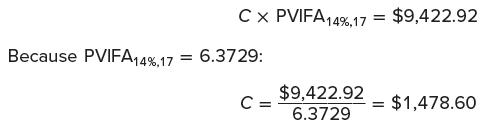

Deposits of $1,478.60 made at the end of each of the first 17 years and invested at 14 percent will provide enough money to make tuition payments of $30,000 over the following four years.

Transcribed Image Text:

20 + Susan's Parents' Parents'... Parents' Tuition Tuition Tuition Tuition birth 1st deposit 0 1 2 2nd deposit 17 18 19 last deposit 21 17th and payment payment payment payment 1 2 3 4