In this exercise, we will learn about the mathematical details underlying many spectral clustering methods (Section 9.4.3). Given an n n n n

In this exercise, we will learn about the mathematical details underlying many spectral clustering methods (Section 9.4.3). Given an $n\times n$ similarity matrix $W$ whose elements are the similarities between the corresponding data tuples (i.e., $W(i,j)$ measures the similarity between tuples $i$ and $j)$. We wish to partition the data tuples into two clusters. Let $q$ be a cluster membership vector of length $n:q\left(i\right)=1$ if data tuple $i$ belongs to Cluster A; and $q\left(i\right)=-1$ if it belongs to Cluster B. One way to find these two clusters is to minimize the so-called cut-size, which measures the total similarities across different clusters:

$$q\ast =\arg \underset{q\in \{-1,1{\}}^n}{min}J=\frac{1}{4}\sum _{i,j=1}^n\left(q\right(i)-q(j\left){)}^{2}W\right(i,j)$$

a. Prove that the cut-size $J=\frac{1}{2}{q}^T(D-W)q$, where $D$ is the degree matrix of $W:D(i,i)=$ ${\sum }_{j=1}^{n}W(i,j)$ and $D(i,j)=0$ for $j\ne i$; and ${}^{}$ is the vector transpose.

b. It is very difficult to directly optimize Eq. (9.48) since the cluster membership vector $q$ is a binary vector. In practice, we relax $q$ and allow it to take real numbers, and aim to solve the following optimization problem instead. Prove that the optimal solution of Eq. (9.49) is given by the eigenvector of $D-W$ that corresponds to the second smallest eigenvalue.

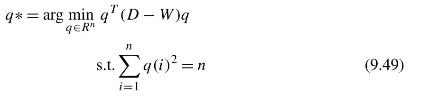
9.4.3 Spectral clustering You may hear that spectral clustering methods have been used in many applications. What is the major idea behind spectral clustering? As discussed in Section 9.2.1, due to the curse of dimensionality, measuring pairwise distance in the original data space of a high-dimensional data set may not be reliable for clustering analysis. Fig. 9.13 illustrates the intuition. The figure shows two clusters of points, one in white and the other in black. Points a and b belong to two different clusters. However, in the original data space, the distance between a and b is shorter than that between a and some other points within the white cluster, such as c. Therefore if we rely on the pairwise distances in the original data space to construct clusters directly, the results may not be meaningful. FIGURE 9.13 0 00 b