It is important to define or select similarity measures in data analysis. However, there is no commonly accepted subjective similarity measure. Results can vary depending on the similarity measures used. Nonetheless, seemingly different similarity measures may be equivalent after some transformation. Suppose we have the following 2-D data set:

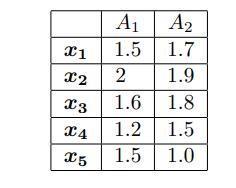
(a) Consider the data as 2-D data points. Given a new data point, x = (1.4, 1.6) as a query, rank the database points based on similarity with the query using Euclidean distance, Manhattan distance, supremum distance, and cosine similarity. (b) Normalize the data set to make the norm of each data point equal to 1. Use Euclidean distance on the transformed data to rank the data points.

x1 x2 X3 X4 X5 A 1.5 2 A 1.7 1.9 1.8 1.6 1.2 1.5 1.5 1.0