Consider again the time-travel problem of the previous exercise, but now consider a greedy algorithm that sorts the men by increasing heights and sorts the spears by increasing heights, and then assigns the ith spear in the ordered list of spears to the ith man in the ordered list of Roman soldiers. Prove or disprove that this greedy strategy results in the optimal assignment of spears to men.

Data From previous exercise.

Suppose you’ve been sent back in time and have arrived at the scene of an ancient Roman battle. Moreover, suppose you have just learned that it is your job to assign n spears to n Roman soldiers, so that each man has a spear. You observe that the men and spears are of various heights, and you have been told (in Latin) that the army is at its best if you can minimize the total difference in heights between each man and his spear. That is, if the ith man has height mi and his spear has height si, then you want to minimize the sum, 

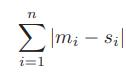
Consider a greedy strategy of repeatedly matching the man and spear that minimizes the difference in heights between these two. Prove or disprove that this greedy strategy results in the optimal assignment of spears to men.

Si >Imi i=1