Question: Suppose there are four power plants, which use coal, nuclear, wind, and oil, and four cities, Flat Top Mountain, Zephyrville, Cherenkov, and Iridescent Islands. The

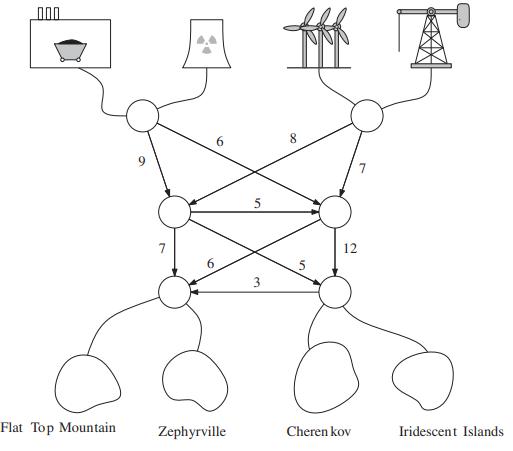
Suppose there are four power plants, which use coal, nuclear, wind, and oil, and four cities, Flat Top Mountain, Zephyrville, Cherenkov, and Iridescent Islands. The power plants and cities are connected by a directed power grid, and each link in the grid has a maximum capacity, as shown in Figure 26.11. Each city demands power with certain constraints. Flat Top Mountain demands 8 units of power, and insists that at least 5 units of this power be from the coal power plant. Zephyrville demands at least 5 units of power and insists that 4 units be generated from wind. Cherenkov demands 8 units of power and insists that 50% of its power be from nuclear power. Iridescent Islands demands at least 6 units of power but wants no more than 2 units of power from oil. Write a linear program to find the maximum flow of power that meets the demands of each city subject to the maximum capacities on the internal links in the power grid.

Figure 26.11

8. 5 7 12 Flat Top Mountain Zephyrville Cheren kov Iridescent Islands

Step by Step Solution

★★★★★

3.41 Rating (167 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To calculate the capacity factor take the total amount of energy the plant produced during a per... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Data Structures Algorithms Questions!

Suppose it has been two years since your graduation. During the time you have worked for a large energy company. In your work, you have been exposed to the numerous ways your employer is investing in...

There are currently 435 nuclear power plants operating worldwide. How many additional nuclear plants would be needed for the world to produce as much commercial energy using nuclear power as we...

Coal is mined and processed at the following four mines in Kentucky, West Virginia, and Virginia: Location .... Capacity (tons) A. Cabin Creek ... 90 B. Surry ..... 50 C. Old Fort ..... 80 D. McCoy...

How did China's economy perform during the first decade of the 2000s? How did joining the WTO contribute to China's economic performance? What economic issues led Wen Jiabao to revise China's...

2/21/2016 A modern ark | The Economist Special report: Climate change Biodiversity A modern ark To save endangered species, move them to more congenial places Nov 28th 2015 | From the print edition...

1. Business and the Environment: Is There More to the Story? by Jane S. Shaw Actions taken to improve the environment are frequently good for profits, but many executives, including economists, are...

The Dutch Flower Cluster The world export market for flowers and flower-related products was almost $30 billion in 2009, having grown more than five-fold since 1998. The Netherlands had been the...

3 COLLEGE ALGEBRA - TRIGONOMETRY Business and Finance (MAT115) This course will start with a review of basic algebra (factoring, solving linear equations, and equalities, etc.) and proceed to a study...

For 20 values of y, it is given that (ax b) = 400 and (bx a) = 545. Given also that x = 6.25, find the value of a and of b.

= 100 kg/mol) is combined with poly(methyl methacrylate) (PMMA, M2 = 75 kg/mol) 4. Polystyrene (M1 in a 25:75 mixture. What is the critical value of the Flory-Huggins parameter for this blend? What...

If two events are mutually exclusive, we know that the probability of their union is the sum of their individual probabilities. However, this is not the case for events that are not mutually...

Aory Company has as old machine with a book walue of $ 3 5 0 0 0 and a nemining fiveysur usaful lfe. Rory is condidering purchasing a new machine at a price of $ 1 0 4 , 0 0 0 . Rory can seil lat old...

Discuss the primary considerations and issues that must be factored into modal and carrier selection.

Give an algorithm for finding the second-to-last node in a singly linked list in which the last node is indicated by a null next reference.

The LinkedPositionalList implementation of Code Fragments 7.97.12 does not do any error checking to test if a given position p is actually a member of the relevant list. Give a detailed explanation...

Suppose we want to extend the PositionalList abstract data type with a method, findPosition(e), that returns the first position containing an element equal to e (or null if no such position exists)....

2. McDaniel Shipyards wants to develop control charts to assess the quality of its steel plate. They take ten sheets of 1" steel plate and compute the number of cosmetic flaws on each roll. Each...

MIPS ASSEMBLY LANGUAGE Write the code of the array with size 20. Assign the elements and display the array elements in reverse order.

Kern Corporation's 5 - year bonds yield 8 . 7 0 % and 5 - year T - bonds yield 5 . 8 0 % . The real risk - free rate is r * = 3 . 3 0 % , the default risk premium for Kern's bonds is DRP = 1 . 6 0 %...