Suppose you work for a computer game company, which is designing a first person shooting game. In this game, players stand just outside of a circular playing field and shoot at targets inside the circle. There are a lot of players and targets, however, so, for any given player, it only makes sense to display the targets that are close by that player. Thus, whenever a new target, t, appears, the game should only make it visible to the players that are in the same “zone” as t. In order to support the fast processing of such queries, you offer to build a binary space partitioning (BSP) tree, T, for use in the game engine. You are given the (x, y) coordinates of all n players, which are in no particular order, but are constrained to all lie at different locations on a circle, C. Your job is to design an efficient algorithm for building such a BSP tree, T, so that its height is O(log n). Thus, the root, r, of T is associated with a line, L, that divides the set of players into two groups of roughly equal size. Then, it should recursively partition each group into two groups of roughly equal size. Describe an O(n log n)-time algorithm for constructing such a tree T. (See Figure 3.17.) 

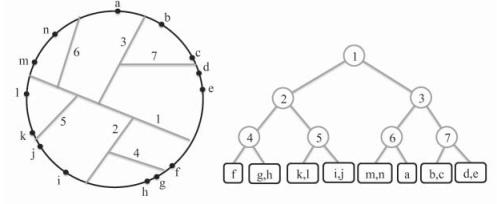
Figure 3.17: A circular environment for a first-person shooter game, where players are represented as points (labeled with letters), together with a two-dimensional BSP tree for this configuration, where dividing lines and nodes are similarly numbered.

Transcribed Image Text:

b 6. 7 m k.l ij a d,e m,n b.c 2.