The greatest common divisor, or GCD, of two positive integers n and m is the largest number j, such that n and m are both multiples of j. Euclid proposed a simple algorithm for computing GCD(n,m), where n > m, which is based on a concept known as the Chinese Remainder Theorem. The main idea of the algorithm is to repeatedly perform modulo computations  of consecutive pairs of the sequence that starts (n,m, . . .), until reaching zero. The last nonzero number in this sequence is the GCD of n and m. For example, for n = 80,844 and m = 25,320, the sequence is as follows:

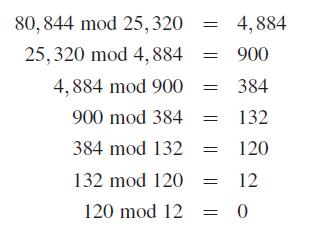
So, GCD of 80,844 and 25,320 is 12. Write a short C++ function to compute GCD(n,m) for two integers n and m.

Transcribed Image Text:

80,844 mod 25, 320 4,884 25,320 mod 4,884 900 4,884 mod 900 384 900 mod 384 132 384 mod 132 120 132 mod 120 12 120 mod 12 = 0