The performance of the radix sort from the previous project can be improved by using more supplementary lists (rather than just list0 and list1).

For example, you can have an array of 16 lists, which we’ll call list[0] through list[15]. Each item of the original list is put into list[index], where the index is computed by the equation:

index = (n >> i) % 16;

During each iteration, you should add 4 to i and multiply the divisor by 16. Reimplement this base 16 version of the radix sort, or use some larger base of your own choosing.

Don’t make the base too big, though, since the number of supplementary lists is equal to the base.

Data from Previous Project

A radix sort is a technique for sorting nonnegative integers (or other data that has individual characters or digits).

One version of radix sort works with a linked list of integers. In addition to the list that is being sorted, there are two extra lists called list0 and list1. The algorithm begins by going through the list of elements to be sorted; every even number is transferred from the original list to the tail of list0, and every odd number is transferred to the tail of list1.

After all numbers have been processed, put the two lists together (with list0 in front and list1 at the back), and then put the whole thing back in the original list.

This process of separating and splicing is repeated a second time, but now we separate based on the boolean expression ((n/2) % 2 == 0). And then we separate and splice using ((n/4) % 2 == 0). And so on, with larger and larger divisors 8, 16, 32, ..., . The process stops when the divisor is bigger than the largest number in the list.

Here is one way to implement the algorithm for ordinary integers (with a maximum value of 231—1):

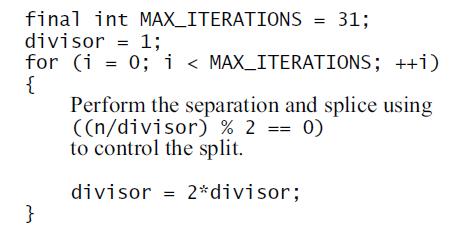
To improve performance, you can break out of the loop if the divisor ever exceeds the largest number in the list. But if you don’t do so, the loop will still end when the divisor overflows the largest possible integer.

The algorithm is quick: Each iteration of the loop takes O(n) time (where n is the size of the list), and the total number of iterations is about log2 m (where m is the maximum number in the list). Thus, the entire time is O(n log m).

Transcribed Image Text:

final int MAX_ITERATIONS = 31; divisor = 1; for (i = 0; i < MAX_ITERATIONS; ++i) { Perform the separation and splice using ((n/divisor) % 2 == 0) to control the split. divisor = 2*divisor; }