Assume the Black-Scholes framework. For t ≥ 0, let S(t) be the time-t price of a stock. You are given:

(i) S(0) = 100.

(ii) The stock’s volatility is 25%.

(iii) The stock pays dividends continuously at a rate proportional to its price. The dividend yield is 2%.

(iv) The continuously compounded expected rate of return on the stock is 6%.

(v) The continuously compounded risk-free interest rate is 5%.

Consider a special 3-year European asset-or-nothing option on the stock. The option’s 3-year payoff is

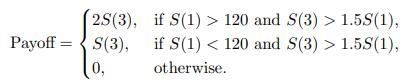
Calculate the time-0 price of this option.

2S(3), Payoff = S(3), 0, if S(1) > 120 and S(3) > 1.5S(1), if S(1) < 120 and S(3) > 1.55S(1), otherwise.