Suppose that there is a single lender and a single borrower, and there is no legal mechanism to enforce loan repayment. A borrower can costlessly keep any amount borrowed, but the lender can then decide not to lend to the borrower in the future. By studying the theory of repeated games discussed in Appendix 1 and by drawing on ideas in Chapter 14, construct a story of how active loan and repayment transactions can be conducted in this credit market.

Data from appendix 1

Another class of intertemporal games that appears more than once in this book is the class of repeated games. A repeated game is easy enough to describe in general terms. Suppose that a set of players is involved in a game (you may choose any of the games that we have discussed so far). Now imagine that this game is played over and over again by the same set of players: it is repeated. Think of this as a giant game in itself. True, the individual games that comprise the giant game are not linked: nothing that you do in any of the minigames influences what the set of players can feasibly achieve in other minigames. Nevertheless, the very fact that the players are involved in the same relationship in the future can be used to influence current play. To see how this works consider two players engaged in repeated play of the Prisoners’ Dilemma. For ready reference we reproduce here the table that makes up a typical Prisoners’ Dilemma:

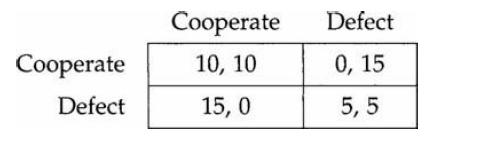
Now we need to introduce the concept of a mental horizon—the notion of some degree of farsightedness on the part of each player. It is absurd to imagine that at any date, each player cares only about her payoff at that date. It is more realistic to suppose that she also worries about her future payoffs. She may care less about payoffs that are far into the future, but the fact remains that she does care. The easiest way to do this is to suppose that a player cares about N periods (including the current one) at every point of time. Thus, if N = 1, she is myopic and cares only about today’s returns. The larger N gets, the larger is the player’s mental horizon.

Transcribed Image Text:

Cooperate Defect Cooperate 10, 10 15, 0 Defect 0, 15 5,5