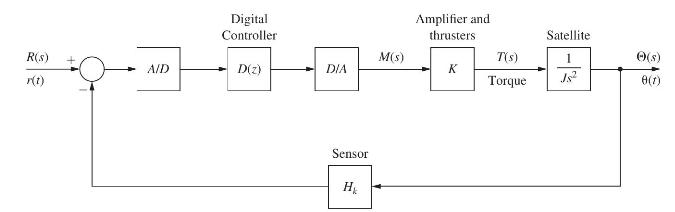
Consider the satellite control system of Problem 5.3-14 and Fig. P5.3-14. Let \(D(z)=2, T=2 \mathrm{~s}, K=4\), \(J=0.2\), and \(H_{k}=0.04\).

(a) Using the closed-loop transfer function, derive a discrete state model for the system.

(b) Derive a discrete state model for the plant from the plant transfer function. Then derive a state model for the closed-loop system by adding the feedback path and system input to a flow graph of the plant.

(c) Calculate the system transfer function from the state model found in part (b), to verify the state model.

(d) Verify the results in part (c) using MATLAB.

Problem 5.3-14

Consider the satellite control system of Fig. P5.3-14. The unit of the attitude angle \(\theta(t)\) is degrees, and the range is 0 to \(360^{\circ}\). The sensor gain is \(H_{k}=0.05\).

Fig. P5.3-14

Transcribed Image Text:

R(s) r(t) Digital Controller Amplifier and thrusters Satellite M(s) T(s) 1 (s) + A/D D(z) DIA K Torque Js 8(t) Sensor Hk