Consider the satellite control system of Problem 9.2-4.

Problem 9.2-4

A satellite control system is modeled as shown in Fig. P9.2-4. This system is described in Problem 1.4-1.
For this problem, let D(z) = 1. In addition, K = 1, T = 1 s, J = 4, and H_k = 1. From the z-transform
tables,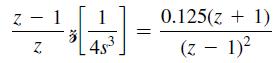

(a) Design a predictor observer for this system, with the time constant equal to one-half the value of Problem 9.2-4(b) and with the observer critically damped.

(b) To check the results of part (a), use (9-46) to show that these results yield the desired observer characteristic equation.

(c) Find the control-observer transfer function $D_{ce}\left(z\right)$ in Fig. 9-8. Use the control gain matrix of Problem 9.2-4(b), $K=\left[\begin{array}{cc}0.3893& 1.769\end{array}\right]$.

(d) The characteristic equation of the closed-loop system of Fig. 9-8 is given by
$$1+D_{ce}\left(z\right)G\left(z\right)=0$$
Use $G\left(z\right)$ as given and $D_{ce}\left(z\right)$ in part (c) to show that this equation yields the same characteristic equation as ${\alpha }_c\left(z\right){\alpha }_e\left(z\right)=0$

I - 2 N 45 0.125(z + 1) (z - 1)