In the conversion of a discrete-time signal to a continuous-time signal, the practical D/A converters, instead of generating impulses at the output, generate a series of pulses \(g(t)\) described by

\[\begin{equation*}x_{\mathrm{p}}(t)=\sum_{n=-\infty}^{\infty} x(n) g(t-n T) \tag{1.243}\end{equation*}\]

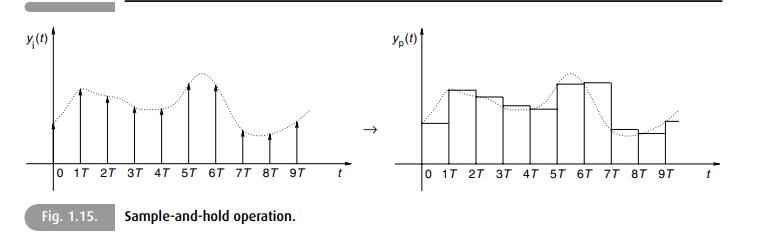
where \(x(n)=x_{\mathrm{a}}(n T)\). For example, in the sample-and-hold operation, which is shown in Figure 1.15, the train of impulses has been replaced by a train of pulses. Assume now that the function \(g(t)\) is

\[g(t)=\left\{\begin{array}{ll}\frac{T-|t|}{T}, & -T \leq t \leq T \\0, & \text { otherwise }\end{array} .\right.\]

For the above choice of pulse \(g(t)\) :

(a) Determine how could the effect of this interpolation be represented in the time domain (see Figure 1.15)?

(b) Determine an expression for the Fourier transform of \(x_{\mathrm{p}}(t)\) in Equation (1.243) as a function of the Fourier transform of \(x_{\mathrm{a}}(t)\).

(c) Determine the frequency response of an ideal lowpass filter that outputs \(x_{\mathrm{a}}(t)\) when \(x_{\mathrm{p}}(t)\) is applied to its input.

Transcribed Image Text:

Y,(t) Yp (!) 0 17 27 37 47 57 67 77 87 0 17 2T 3T 4T 5T 6T 7T 8T 9T Fig. 1.15. Sample-and-hold operation.