Repeat Exercise 5.25 with the following order estimate (Kaiser, 1974): [M approx frac{-20 log _{10}left(sqrt{delta_{mathrm{p}} delta_{mathrm{r}}} ight)-13}{2.3237left(omega_{mathrm{r}}-omega_{mathrm{p}}

Question:

Repeat Exercise 5.25 with the following order estimate (Kaiser, 1974):

\[M \approx \frac{-20 \log _{10}\left(\sqrt{\delta_{\mathrm{p}} \delta_{\mathrm{r}}}\right)-13}{2.3237\left(\omega_{\mathrm{r}}-\omega_{\mathrm{p}}\right)}+1\]

where \(\omega_{\mathrm{p}}\) and \(\omega_{\mathrm{r}}\) are the digital passband and stopband edges. Which estimate tends to be more accurate?

Exercise 5.25

The following relationship estimates the order of a lowpass filter designed with the minimax approach (Rabiner et al., 1975). Design a series of lowpass filters and verify the validity of this estimate ( \(\Omega_{\mathrm{s}}\) is the sampling frequency):

\[M \approx \frac{D_{\infty}\left(\delta_{\mathrm{p}}, \delta_{\mathrm{r}}\right)-f\left(\delta_{\mathrm{p}}, \delta_{\mathrm{r}}\right)(\Delta F)^{2}}{\Delta F}+1\]

where

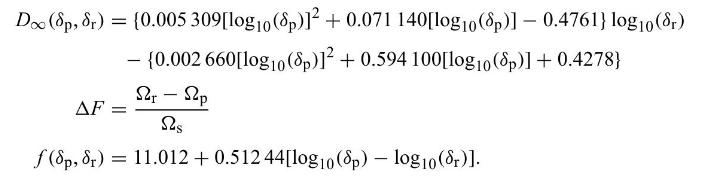
image text in transcribed