A tank (Figure P1.11) with mass (m_{1}=2,000 mathrm{~kg}) fires a cannon with mass (m_{2}=2 mathrm{~kg}) and velocity
Question:
A tank (Figure P1.11) with mass \(m_{1}=2,000 \mathrm{~kg}\) fires a cannon with mass \(m_{2}=2 \mathrm{~kg}\) and velocity \(=10 \mathrm{~m} / \mathrm{sec}\). The recoil mechanism consists of a spring with stiffness \(=11,000 \mathrm{~N} / \mathrm{m}\), and a damper. There are three possible values of the damping coefficient: \(0.2 c_{c}, c_{c}\), and \(1.5 c_{c}\) where \(c_{c}\) is the critical damping.
Figure P1.11
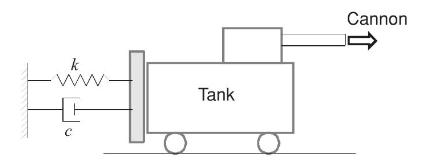
a. For each value of the damping constant, determine the time required to come back to the original firing position. Validate your analytical results via comparison with results from numerical integration of the solution of the differential equation via MATLAB.
b. What will be your recommendation regarding the choice of the damping coefficient? Explain your answer.
Step by Step Answer:






