Prediction in the one-way random effects model. (a) For the predictor (y_{i, T+S}) given in (2.37), compute
Question:
Prediction in the one-way random effects model.
(a) For the predictor \(y_{i, T+S}\) given in (2.37), compute \(E\left(u_{i, T+S} u_{i t}ight)\) for \(t=\) \(1,2, \ldots, T\) and verify that \(w=E\left(u_{i, T+S} uight)=\sigma_{\mu}^{2}\left(l_{i} \otimes \iota_{T}ight)\) where \(l_{i}\) is the \(i\) th column of \(I_{N}\).
(b) Verify (2.39) by showing that \(\left(l_{i}^{\prime} \otimes \iota_{T}^{\prime}ight) P=\left(l_{i}^{\prime} \otimes \iota_{T}^{\prime}ight)\).
![]()
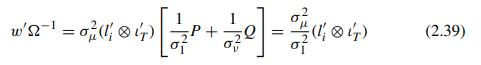
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





