Question: (Generalized Pythagorean Theorem) Let A he a nonsingular symmetric matrix such that z'Az > 0 for all ze RN, z0. Confirm that X'AX is nonsingular

(Generalized Pythagorean Theorem) Let A he a nonsingular symmetric matrix such that z'Az > 0 for all ze RN, z0. Confirm that X'AX is nonsingular and that

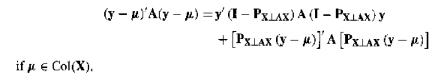
if = Col(X). (y)A(y p) y (I-PxLAX) A (I - PXLAX) y

if = Col(X). (y)A(y p) y (I-PxLAX) A (I - PXLAX) y +[PXLAX (y-M)]'A [PXLAX (y - p)]

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Econometric Analysis Questions!

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Least Squares Approximation Hector D. Ceniceros 1 Least Squares Approximation Let f be a continuous function on [a, b]. We would like to find the best approximation to f by a polynomial of degree at...

Submitted to Management Science manuscript MS-0001-1922.65 Authors are encouraged to submit new papers to INFORMS journals by means of a style file template, which includes the journal title....

Please help me solve the following 8 questions so that I can compare it with my answers Throughout this module, we have assumed that SSE/o' ~ Xn-p; however, we have never seen a proof for it! We now...

Show the parse trees for the two parses that the grammar assigns for sentence S1. S1: the train station bus rumbles [3 marks] (b) Give an algorithm for a bottom-up passive chart parser without...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Jason uses the following steps to construct a perpendicular line through a point C on a line segment. Step 1: From point C, draw an arc intersecting the line segment in points A and B. Step 2: Using...

1. As we saw with Merge Sort, often see time (or space) complexity written as a recurrence relation (think of any recursive algorithm). In class to determine the complexity in asymptotic notation of...

Please help me to answer this question, not even sure where to begin. Thanks in advance 3. Pappus's Variation on the Pythagorean Theorem: Let A ABC be a triangle (not necessarily a right triangle)....

Sarah Lee (SL) manufactures cakes. Its main product is a frozen butter cake. SL uses normal costing and weighted average process costing. It closes MOH variance to Cost of Goods Sold (COGS) at the...

For any two vectors and v, xv is solenoidal if O is solenoidal but is not O is solenoidal whereas is irrotational O and v are both solenoidal O and are both irrotational

The direct write off method is : Better matching. Theoretically undesirable Receivable stated at cash realizable value. Required by GAAP

Solve the linear programming problems stated in Problem Minimize and maximize z = 400x + 100y subject to 3x - y 24 x + 2y 16 y 30 x, y 0