Consider the binary variable version of the fixed effects model in Equation (10.11) except with an additional
Question:
Consider the binary variable version of the fixed effects model in Equation (10.11) except with an additional regressor, \(D 1_{i}\); that is, let
\[ Y_{i t}=\beta_{0}+\beta_{1} X_{i t}+\gamma_{1} D 1_{i}+\gamma_{2} D 2_{i}+\cdots+\gamma_{n} D n_{i}+u_{i t} \]
a. Suppose that \(n=3\). Show that the binary regressors and the "constant" regressor are perfectly multicollinear; that is, express one of the variables \(D 1_{i}, D 2_{i}, D 3_{i}\), and \(X_{0, i t}\) as a perfect linear function of the others, where \(X_{0, i t}=1\) for all \(i, t\).
b. Show the result in (a) for general \(n\).
c. What will happen if you try to estimate the coefficients of the regression by OLS?
Equation (10.11)
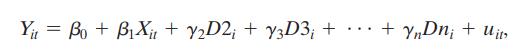
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





