Consider the cointegrated model \(Y_{t}=\theta X_{t}+v_{1 t}\) and \(X_{t}=X_{t-1}+v_{2 t}\), where \(v_{1 t}\) and \(v_{2 t}\) are mean 0 serially uncorrelated random variables with \(E\left(v_{1 t} v_{2 j}\right)=0\) for all \(t\) and \(j\). Derive the vector error correction model [Equations (17.22) and (17.23)] for \(X\) and \(Y\).

Equations (17.22)

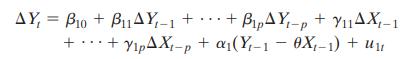
Equations (17.23)

Transcribed Image Text:

= AY, B10 B11AY-1++ BAY-p + AX-1 + + YX-p + a(Y-10X1-1) + u11 -P