Detecting autocorrelation: von Neumann ratio test.* Assuming that the residual û_tare random drawings from normal distribution, von Neumann has shown that for large n, the ratio

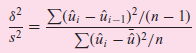
called the von Neumann ratio, is approximately normally distributed with mean

and variance

a. If n is sufficiently large, how would you use the von Neumann ratio to test for autocorrelation?

b. What is the relationship between the Durbin€“Watson d and the von Neumann ratio?

c. The d statistic lies between 0 and 4. What are the corresponding limits for the von Neumann ratio?

d. Since the ratio depends on the assumption that the uÌ‚€™s are random drawings from normal distribution, how valid is this assumption for the OLS residuals?

e. Suppose in an application the ratio was found to be 2.88 with 100 observations. Test the hypothesis that there is no serial correlation in the data.

B. I. Hart has tabulated the critical values of the von Neumann ratio for sample sizes of up to 60 observations.

Transcribed Image Text:

δ Σ 1-i-ι)?/(π - 1) Σ t, -i)/n Γe 82 2n n – 1