Suppose (Y_{i}=beta X_{i}+u_{i}), where ( (left.u_{i}, X_{i} ight)) satisfy the Gauss-Markov conditions given in Equation (5.31). a.
Question:
Suppose \(Y_{i}=\beta X_{i}+u_{i}\), where ( \(\left.u_{i}, X_{i}\right)\) satisfy the Gauss-Markov conditions given in Equation (5.31).
a. Derive the least squares estimator of \(\beta\), and show that it is a linear function of \(Y_{1}, \ldots, Y_{n}\).
b. Show that the estimator is conditionally unbiased.
c. Derive the conditional variance of the estimator.
d. Prove that the estimator is BLUE.
Equation (5.31)
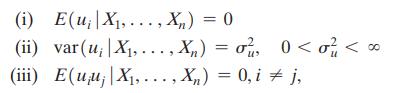
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





