The discussion following Equation (8.28) interprets the coefficient on interacted binary variables using the conditional mean zero
Question:
The discussion following Equation (8.28) interprets the coefficient on interacted binary variables using the conditional mean zero assumption. This exercise shows that this interpretation also applies under conditional mean independence. Consider the hypothetical experiment.
a. Suppose you estimate the regression \(Y_{i}=\gamma_{0}+\gamma_{1} X_{1 i}+u_{i}\) using only the data on returning students. Show that \(\gamma_{1}\) is the class size effect for returning students - that is, that \(\gamma_{1}=E\left(Y_{i} \mid X_{1 i}=1, X_{2 i}=0\right)\) \(E\left(Y_{i} \mid X_{1 i}=0, X_{2 i}=0\right)\). Explain why \(\hat{\gamma}_{1}\) is an unbiased estimator of \(\gamma_{1}\).
b. Suppose you estimate the regression \(Y_{i}=\delta_{0}+\delta_{1} X_{1 i}+u_{i}\) using only the data on new students. Show that \(\delta_{1}\) is the class size effect for new students - that is, that \(\delta_{1}=E\left(Y_{i} \mid X_{1 i}=1, X_{2 i}=1\right)-E\left(Y_{i} \mid X_{1 i}=0\right.\), \(\left.X_{2 i}=1\right)\). Explain why \(\hat{\delta}_{1}\) is an unbiased estimator of \(\delta_{1}\).
c. Consider the regression for both returning and new students, \(Y_{i}=\beta_{0}+\beta_{1} X_{1 i}+\beta_{2} X_{2 i}+\beta_{3}\left(X_{1 i} \times X_{2 i}\right)+u_{i}\). Use the conditional mean independence assumption \(E\left(u_{i} \mid X_{1 i}, X_{2 i}\right)=E\left(u_{i} \mid X_{2 i}\right)\) to show that \(\beta_{1}=\gamma_{1}, \beta_{1}+\beta_{3}=\delta_{1}\), and \(\beta_{3}=\delta_{1}-\gamma_{1}\) (the difference in the class size effects).
d. Suppose you estimate the interaction regression in (c) using the combined data and \(E\left(u_{i} \mid X_{1}, X_{2 i}\right)=E\left(u_{i} \mid X_{2 i}\right)\). Show that \(\hat{\beta}_{1}\) and \(\hat{\beta}_{3}\) are unbiased but that \(\hat{\beta}_{2}\) is, in general, biased.
Equation (8.28)
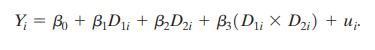
Step by Step Answer:






