Develop a mathematical relationship for finding the accumulated amount F at the end of n years of a gradient series where the interest is i%. Put differently, you already have access to a (P|G i%;n) factor. Develop an (F|G i%;n) factor.

a. Express the (F|G i%;n) factor in terms of the existing factors listed in the tables of Appendix A.

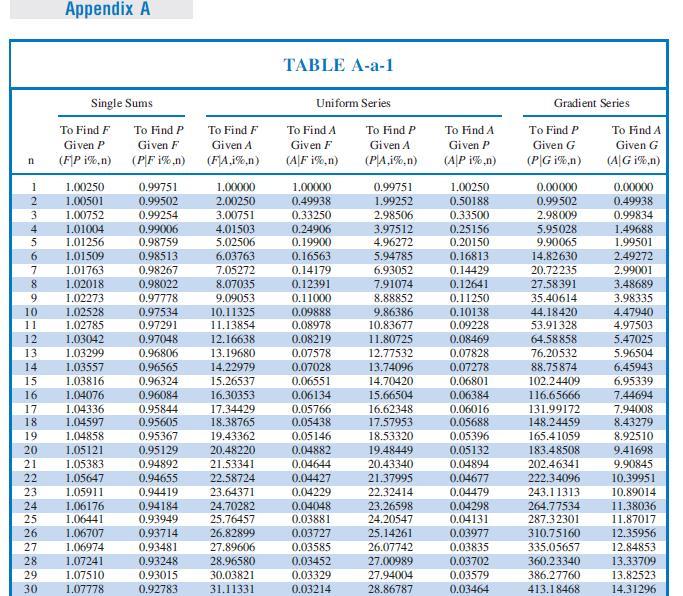
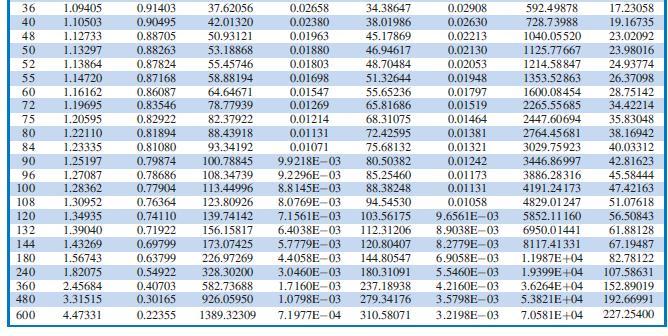
b. Express the (FjG i%;n) factor in terms of i and n.

c. Demonstrate that your answers to (a) and (b) are equivalent by calculating the value of F using a first payment of \($0\), increasing by \($1\),000 each year with n = 5 and i = 10 percent for each approach.

Transcribed Image Text:

Appendix A TABLE A-a-1 Uniform Series Given P Single Sums To Find F To Find P Given F To Find F To Find A To Find P To Find A Given A Given F n (FP i%,n) (PF i%,n) (FA,i%,n) (A|Fi%,n) Given A (PA,i%.n) Given P (A|P i%,n) Gradient Series To Find P Given G (P|Gi%,n) To Find A Given G (A|Gi%,n) 1 1.00250 0.99751 1.00000 1.00000 0.99751 1.00250 0.00000 0.00000 2 1.00501 0.99502 2.00250 0.49938 1.99252 0.50188 0.99502 0.49938 3 1.00752 0.99254 3.00751 0.33250 2.98506 0.33500 2.98009 0.99834 4 1.01004 0.99006 4.01503 0.24906 3.97512 0.25156 5.95028 1.49688. 5 1.01256 0.98759 5.02506 0.19900 4.96272 0.20150 9.90065 1.99501 6 1.01509 0.98513 6.03763 0.16563 5.94785 0.16813 14.82630 2.49272 7 1.01763 0.98267 7.05272 0.14179 6.93052 0.14429 20.72235 2.99001 8 1.02018 0.98022 8.07035 0.12391 7.91074 0.12641 27.58391 3.48689 9 1.02273 0.97778 9.09053 0.11000 8.88852 0.11250 35.40614 3.98335 10 1.02528 0.97534 10.11325 0.09888 9.86386 0.10138 44.18420 4.47940 11 1.02785 0.97291 11.13854 0.08978 10.83677 0.09228 53.91328 4.97503 12 1.03042 0.97048 12.16638 0.08219 11.80725 0.08469 64.58858 5.47025 13 1.03299 0.96806 13.19680 0.07578 12.77532 0.07828 76.20532 5.96504 14 1.03557 0.96565 14.22979 0.07028 13.74096 0.07278 88.75874 6.45943 15 1.03816 0.96324 15.26537 0.06551 14.70420 0.06801 102.24409 6.95339 16 1.04076 0.96084 16.30353 0.06134 15.66504 0.06384 116.65666 7.44694 17. 1.04336 0.95844 17.34429 0.05766 16.62348 0.06016 131.99172 7.94008 18 1.04597 0.95605 18.38765 0.05438 17.57953 0.05688 148.24459 8.43279 19 1.04858 0.95367 19.43362 0.05146 18.53320 0.05396 165.41059 8.92510 20 1.05121 0.95129 20.48220 0.04882 19.48449 0.05132 183.48508 9.41698 21 1.05383 0.94892 21.53341 0.04644 20.43340 0.04894 202.46341 9.90845 22 1.05647 0.94655 22.58724 0.04427 21.37995 0.04677 222.34096 10.39951 23 1.05911 0.94419 23.64371 0.04229 22.32414 0.04479 243.11313 10.89014 24 1.06176 0.94184 24.70282 0.04048 23.26598 0.04298 264.77534 11.38036 25 1.06441 0.93949 25.76457 0.03881 24.20547 0.04131 287.32301 11.87017 26 1.06707 0.93714 26.82899 0.03727 25.14261 0.03977 310.75160 12.35956 27 1.06974 0.93481 27.89606 0.03585 26.07742 0.03835 335.05657 12.84853 28 1.07241 0.93248 28.96580 0.03452 27.00989 0.03702 360.23340 13.33709 29 1.07510 0.93015 30.03821 0.03329 27.94004 0.03579 386.27760 13.82523 30 1.07778 0.92783 31.11331 0.03214 28.86787 0.03464 413.18468 14.31296