OABC is a square. M is the midpoint of OA, and Q divides BC in the ratio
Question:
OABC is a square. M is the midpoint of OA, and Q divides BC in the ratio 1 : 3. AC and MQ meet at P.
a. If OA(vector) = a and OC(vector) = c, express OP(vector) in terms of a and c.
b. Show that P divides AC in the ratio 2 : 3.
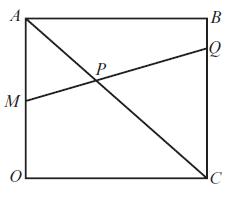
Transcribed Image Text:
A M B 12 C
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 0% (5 reviews)
To solve this problem lets break it down step by step a To find OPvector in terms of a and c we need to analyze the given information Since M is the m...View the full answer

Answered By

ROXAN VEGA
I have extensive hands-on experience and proficiency in assisting students in various subjects. During my tutoring sessions, I prioritize creating a supportive and engaging learning environment. I strive to understand each student's unique learning style and tailor my teaching methods accordingly. I am patient, empathetic, and skilled at breaking down complex concepts into simpler, more manageable parts. I encourage active participation and discussion, promoting critical thinking and problem-solving skills.
One of my strengths as a tutor is my ability to adapt to different learning needs and styles. I can explain difficult concepts using real-life examples, visual aids, or interactive exercises, depending on what works best for the student. I also provide clear explanations, answer questions, and offer guidance in a clear and concise manner.
0.00
0 Reviews
10+ Question Solved
Related Book For 

Edexcel AS And A Level Mathematics Pure Mathematics Year 1/AS
ISBN: 9781292183398
1st Edition
Authors: Greg Attwood
Question Posted:
Students also viewed these Mathematics questions
-
Solve the linear programming problems in Problem by applying the simplex method to the dual problem. Minimize C = 7x1 + 5x2 %3D subject to X1 + x2 2 4 X - 2x, 2 -8 -2x, + x, 2 -8 | X1, X2 2
-
Sketch a graph of f(t) = e t on an arbitrary interval [a, b]. Use the graph and compare areas of regions to prove that eb ea e + eb ela+b)/2 < b a 2
-
A pair of straight teeth spur gears is to transmit 20 kW when the pinion rotates at 300 rpm. The velocity ratio is 3. The allowable stresses for the pinion and gear materials are 120 MPa and 100 MPa,...
-
In Exercises verify the identity. coshx = 1 + cosh 2x 2
-
BMW Group, headquartered in Munich, Germany, manufactures several automotive brands including BMW Group, MINI, and Rolls-Royce. Financial information is reported in the euro () monetary unit using...
-
(a) Find the approximations TS and MS for the integral (b) Estimate the errors in the approximations of part (a). (c) How large do we have to choose n so that the approximations Tn and Mn to the...
-
How do you select the appropriate statistical method to test a hypothesis?
-
Your client is a company that owns a shopping center with 30 store tenants. All leases with the store tenants provide for a fixed rent plus a percentage of sales, net of sales taxes, in excess of a...
-
P Ltd acquired 70% of S Ltd three years ago, when S Ltd.s retained earnings were GHS430,000. The financial statements of each company for the year ended 31 March 2017 are as follows: Statements of...
-
What do you see as advantages and disadvantages of do-it yourself process flows, such as self-checkout at grocery stores?
-
In triangle ABC the position vectors of the vertices A, B and C are Find: a. |AB(vector) b. |AC(vector)| c. |BC(vector)| d. The size of BAC, ABC and ACB to the nearest degree. (3), (3) and (7).
-
ABCD is a trapezium with AB parallel to DC and DC = 4AB. M divides DC such that DM : MC = 3 : 2, AB(vector) = a and BC(vector) = b. Find, in terms of a and b: 1 a AM b BD MB d DA
-
Evelyn Everest gave property to her mother Sharon when the adjusted basis of the property was $12,000 and the fair market value was $80,000. Sharon died eight months later when the property was...
-
Directions: Put your feet in the shoes of the business owner and suggest specific ways on how a business can gain profit and how it can be avoid loss Ways to Gain Profit 1. 2. 3. 4. 5. 1. 2. 3. 4. 5....
-
Define business intelligence Briefly discuss how your organisation can use business intelligence to improve decision-making Please see below rubric as guidance. Kindly list references in APA 7th...
-
Mr Santos apply for college educational plan for his 3 children .The 3 children ages are 6 yrs old , 3 yrs old and 1 yr old. The fund will be set-up the deposit of a fixed sum on the child's current...
-
Recovery Centers of America needs to acquire new vehicles that will cost $2.5 million across its six state service area. It plans to use the vehicles for three years, at which time new vehicles will...
-
The following program is supposed to allow the user to enter a list of numbers, then print them out formatted with 2 decimal positions. However, there are 3 errors. Indicate the line number of each...
-
Willis Construction, Inc., completed the following transactions during June 2016, its first month of operations: Jun 2 Sold $10,000 of common stock to Davis Willis to start the construction business....
-
Select the correct answer for each of the following questions. 1. On December 31, 20X3, Saxe Corporation was merged into Poe Corporation. In the business combination, Poe issued 200,000 shares of its...
-
It is well known that on average women live about four years longer than men. However, are they healthier? Conduct a test to determine if women (SEX: 1 = Male, 2 = Female) consider themselves to be...
-
Can we infer that women are more likely than men to lose their jobs in the next 12 months (JOBLOSE: In the next 12 months how likely is it that you will lose your job or be laid off: 1 = Very likely,...
-
Refer to Exercise 19.24. Is there sufficient evidence to infer that people who work for themselves (WRKSLF: 1 = Self-employed, 2 = Work for someone else) differ from those who work for someone else...
-
QUESTION 3 A business owns seven flats rented out to staff at R500 per month. All flats were tenanted Ist january 21 months rent was in arrears and as at 31st December 14 months' rent wa Identify the...
-
1. 2. 3. Select the Tables sheet, select cells A6:B10, and create range names using the Create from Selection button [Formulas tab, Defined Names group]. Select cells B1:F2 and click the Name box....
-
Tropical Rainwear issues 3,000 shares of its $18 par value preferred stock for cash at $20 per share. Record the issuance of the preferred shares. (If no entry is required for a particular...

Study smarter with the SolutionInn App


