FREE Trial

Consider a stress function formulation for the axisymmetric problem discussed in Section 14.2. The appropriate compatibility relation

Question:

Consider a stress function formulation for the axisymmetric problem discussed in Section 14.2. The appropriate compatibility relation for this case has been previously developed in Example 8.11; see (8.4.76). Using the plane stress Hooke’s law, express this compatibility relation in terms of stress and then in terms of the Airy function to get the result:

0= d dr2 2011) (2-[(-(-3) (4]

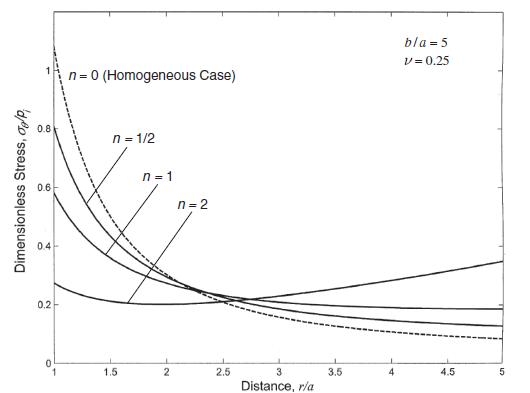
Data from section 14.2

We start our study by re-examining Example 8.6, a plane axisymmetric problem of a hollow cylin- drical domain

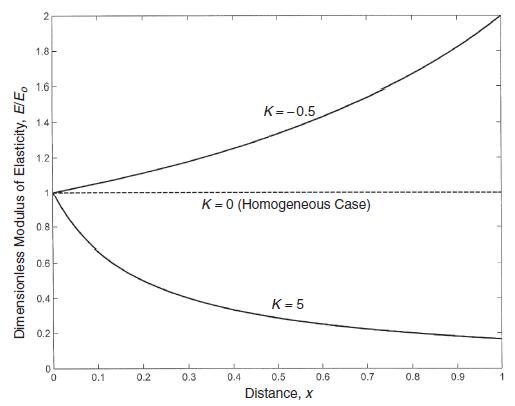
Dimensionless Modulus of Elasticity, E/E, 2 1.8- 1.6 1.4- 1.2 0.8 0.6 0.4 0.2 8 0 0.1 0.2 0.3 K=-0.5 K = 0

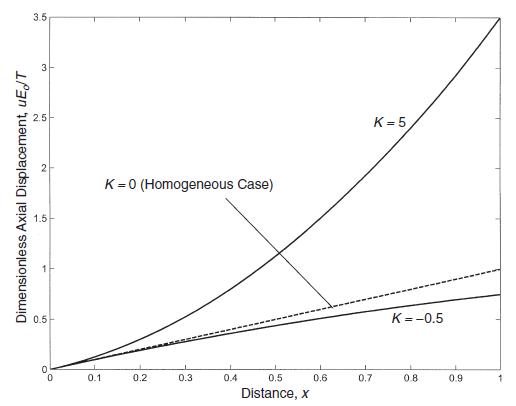
Dimensionless Axial Displacement, uE/T 3.5 2.5 1.5- 0.5- 0 0.1 K = 0 (Homogeneous Case) 0.2 0.3 0.4 0.5

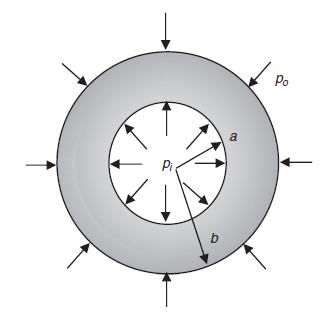
Pi b a Po

Or = de E(r) [du 1- (r) dr E(r) 1-v(r) +v(r = du [+(r)]) dr Note that the corresponding plane strain

where E, and n are constants and a is the inner boundary radius. Note that Eo has the same units as E and as

Dimensionless Young's Modulus, E/E 15 10 n = 0 (Homogeneous Case) 1.5 2 n=2 2.5 3.5 Dimensionless Distance,

This particular gradation model reduces the Navier equation (14.2.2) to du (n+1) du dr + dr r The solution to

As with the homogeneous example, we choose the special case with only internal pressure (po = 0), which gives

which matches with the solution shown in Fig. 8.9 for bla = 2. A plot of the nondimensional stress

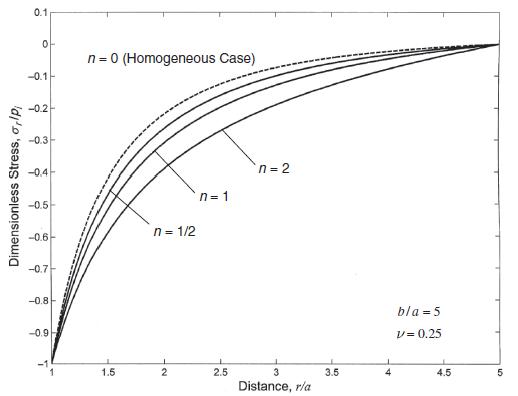
Dimensionless Stress, , p 0.1 of -0.1- -0.2 -0.3 -0.4 -0.5- -0.6- -0.7- -0.8 -0.9 n = 0 (Homogeneous Case)

Dimensionless Stress, P 0.8 0.6 0.4 0,2 0 n = 0 (Homogeneous Case) n = 1/2 1.5 n=1 L 2 n=2 2.5 3 Distance,

corresponding results for the tangential stress shown in Fig. 14.8 show much more marked differences. WhileData from example 8.11

As a final example in this section, consider the problem of a thin uniform circular disk subject to constant

y a (0) X

The solution can be efficiently handled by using a special stress function that automatically satisfies the

Recall that the more general polar coordinate case was given as Exercise 7.17. Using Hooke's law for plane

Equation 8.4.76

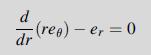
d dr (rea) er = 0 -

Transcribed Image Text:

0= dr2 d 102 1) (2 -[(-(-3) (4]

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Answer rating: 25% (4 reviews)

Hookes Law plane stress e lo 1 E...View the full answer


answer-question-section
Answered By
tutor-profile-image
Ehsan Mahmood
I’ve earned Masters Degree in Business Studies and specialized in Accounts & Finance. Couple with this, I have earned BS Sociology from renowned institute of Pakistan. Moreover, I have humongous teaching experience at Graduate and Post-graduate level to Business and humanities students along with more than 7 years of teaching experience to my foreign students Online. I’m also professional writer and write for numerous academic journals pertaining to educational institutes periodically.
4.90+ 248+ Reviews 287+ Question Solved
Related Book For  book-img-for-question
Elasticity Theory Applications And Numerics

Elasticity Theory Applications And Numerics

ISBN: 9780128159873

4th Edition

Authors: Martin H. Sadd Ph.D.

See More Books
Question Posted:
See More Questions

Students also viewed these Engineering questions

Static And Dynamic Performance Limitations For High Speed D/A Converters 2004 Edition - ISBN: 1441954341 - Free Book